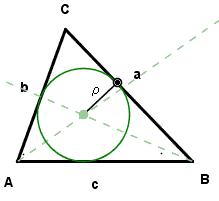
Inscribed circle
Calculate the magnitude of the BAC angle in triangle ABC if it is three times less than the angle BOC, where O is the center of the circle inscribed in triangle ABC.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Semicircle
The semicircle with center S and the diameter AB is constructed equilateral triangle SBC. What is the magnitude of the angle ∠SAC? - Quadrilateral 82395
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - Triangle 15123
In triangle ABC, we know the angle BAC = 50 degrees. What is the angle between the axis of the angle ACB and the axis of the angle CAB? - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
- Magnitude 29891
The triangle ABC is the magnitude of the inner angle α 12 ° smaller than the angle β, and the angle γ is four times larger than the angle α. What size are these interior angles in the triangle? - Three angles
In a triangle ABC, the magnitude of the internal angle gamma is equal to one-third of the angle alpha. The size of the angle beta is 80 degrees larger than the size of the gamma angle. Calculate the magnitudes of the interior angles of the triangle ABC. - Isosceles 71154
Calculate all interior angles in the isosceles triangle ABC if we know that BC is the base, and we also know: | ∢BAC | = α; | CABCA | = 4α
