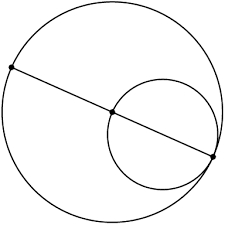
The ratio
The ratio of the lengths of the two circles is 5:2. Find the ratio of a
a) the radii of these circles
b) the areas for these circles
a) the radii of these circles
b) the areas for these circles
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangular triangles
The lengths of the corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and - Common chord
Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles? - Circles
The areas of the two circles are in the ratio 5:10. The larger circle has a diameter of 14. Calculate the radius of the smaller circle. - The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm.
- Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Intersect 6042
Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles? - Difference 80618
A regular hexagon is described and inscribed in a circle. The difference between its areas is 8√3. Find the circle's radius.
