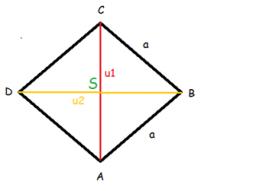
Diamond diagonals

Calculate the diamonds' diagonals lengths if the diamond area is 156 cm square and the side length is 13 cm.

Result

u =  21.633 cm
v =  14.422 cm

Solution:


Checkout calculation with our calculator of quadratic equations.

v=x2=208=4 13≐14.4222=14.422  cm v = \sqrt{ x_{ 2 } } = \sqrt{ 208 } = 4 \ \sqrt{ 13 } \doteq 14.4222 = 14.422 \ \text{ cm }

Try another example


Our examples were largely sent or created by pupils and students themselves. Therefore, we would be pleased if you could send us any errors you found, spelling mistakes, or rephasing the example. Thank you!





Leave us a comment of this math problem and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




Tips to related online calculators
Looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have quadratic equation?
Pythagorean theorem is the base for the right triangle calculator.

Following knowledge from mathematics are needed to solve this word math problem:

Next similar math problems:

  1. Diamond and diagonals
    kosostvorec A diamond has diagonals f = 8 cm and g = 6 cm long. How long is this diamond perimeter? (Calculate it!)
  2. Diamond diagonals
    kosodlznik_2 Find the diamond diagonal's lengths if the area is 156 cm2 and side is 13 cm long.
  3. Diagonals of diamond
    kosostvorec_4 Find the area and circumference of the diamond ABCD with 15m and 11m diagonals.
  4. Park
    diamond_3 In the park is marked diamond shaped line connecting locations A, D, S, C, B, A. Calculate its length if |AB| = 108 m, |AC| = 172.8 m.
  5. Diagonals in diamons/rhombus
    diamonds Rhombus ABCD has side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal.
  6. Diagonals of a rhombus
    rhombus-diagonals_1 One of the diagonals of a rhombus is twice as the other. If the sum of the lengths of the diagonals is 24, find the area of the rhombus.
  7. Rhombus
    kosostvorec_1 The rhombus has diagonal lengths of 4.2cm and 3.4cm. Calculate the length of the sides of the rhombus and its height
  8. Diagonal to area
    rectangle_5 Calculate the area of a rectangle in which the length of the diagonal is 10 cm.
  9. Square diagonal
    square_diagonal Calculate the length of diagonal of the square with side a = 23 cm.
  10. Equilateral triangle
    rs_triangle_1 The equilateral triangle has a 23 cm long side. Calculate its content area.
  11. Triangle
    Triangle_trig Calculate the sides of the triangle if its area S = 630 and the second cathethus is shorter by 17.
  12. Rhombus diagonal
    rhombus2_1 Area of rhombus is 224. One diagonal measures 33, find length of other diagonal.
  13. Satin
    diagonal_rectangle_3 Sanusha buys a piece of satin 2.4 m wide. The diagonal length of the fabric is 4m. What is the length of the piece of satin?
  14. Fifth of the number
    numbs_5 The fifth of the number is by 24 less than that number. What is the number?
  15. A mast
    stoziar_1 A mast 32 meters high was broken by the wind so that its top touches the ground 16 meters from the pole. The still standing part of the mast, the broken part and the ground form a rectangular triangle. At what height was the mast broken?
  16. Holidays - on pool
    pool_4 Children's tickets to the swimming pool stands x € for an adult is € 2 more expensive. There was m children in the swimming pool and adults three times less. How many euros make treasurer for pool entry?
  17. Column
    pole_phone Perpendicular pole high 8 m tall broke and its toe fell 2.7 m from the bottom of the pole. At what height above the ground pole broke?