14 sticks
I was cleaning up my attic recently and found a set of at least 14 sticks which a curious Italian sold me some years ago. Trying hard to figure out why I bought it from him, I realized that the set has the incredible property that there are no three sticks that can form a triangle. If the set has two sticks of length 1, which are the smallest, what is the least possible length of the 14th stick?
Correct answer:
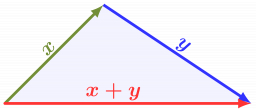
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Reducing scale
I am sizing some landscaping, and I measured everything on a 20 to 1 scale. I realized when I was done that it was at 30 to 1. How can I convert what I already have to 30 to 1. For example, if the grass area is 22,871.6' at 20 to 1, how do you figure it o - Hypotenuse 79904
I have a right triangle, the length of the hypotenuse is c 20, and I only know the side ratio a:b = 2:1. I can't figure out the actual length of the hangers = I'm already an old man, and my brain doesn't work at 100% like it did years ago at school - I co - Inaccurate 34503
Peter has an inaccurate alarm clock. He found that he was exactly 4 minutes late every hour. At 21:30 in the evening, he will set the exact time for it. What must alarm time be on him to wake him up at exactly 06:30? - Cards
From a set of 32 cards, we randomly pull out three cards. What is the probability that it will be seven kings and an ace?
- Performance 4403
During a public performance, majorettes line up in three-step, four-step, six-step, and eight-step. All rows are full with each grouping, and no majorette is promoted. Determine the smallest possible number of majorettes for which a performance can be mad - Odd-numbered 4033
Mr. O. came up with two codes for the vault, which he alternates after a week. Both codes have the product of the digit 120. In an even week, it uses the smallest possible number as the code with this property. In the odd week, the largest. No number 1 in - Triangle from sticks
Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks?
