Podkrovie
Nedávno som upratoval podkrovie a našiel som sadu najmenej 14 palíc, ktoré mi pred pár rokmi predal jeden zvedavý Talian. Keď som sa usilovne snažil prísť na to, prečo som to od neho kúpil, uvedomil som si, že sada má tú neuveriteľnú vlastnosť, že neexistujú 3 paličky, ktoré by vytvorili trojuholník. Ak má sada dve paličky dĺžky 1, ktoré sú najmenšie, aká je najmenšia možná dĺžka 14. palice?
Správna odpoveď:
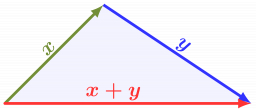
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikaplanimetriazákladné operácie a pojmyÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Pravouhlý trojuholník
 Mám pravouhlý trojuholník, dĺžka prepony c 20 a poznám len pomer strán a:b = 2:1. nemôžem prísť na skutočnú dĺžku tých odvesení = sem už staršia člobrda a mozog už mi nešliape na 100% ako pred rokmi na škole - vtedy by som to určite zvládol...
Mám pravouhlý trojuholník, dĺžka prepony c 20 a poznám len pomer strán a:b = 2:1. nemôžem prísť na skutočnú dĺžku tých odvesení = sem už staršia člobrda a mozog už mi nešliape na 100% ako pred rokmi na škole - vtedy by som to určite zvládol... - Vyfarbi
 Napíš na papier čísla od 0 do 31. Ak sa dve čísla líšia o 3, vyfarbi ich rovnako. Koľko si vyfarbil dvojíc?
Napíš na papier čísla od 0 do 31. Ak sa dve čísla líšia o 3, vyfarbi ich rovnako. Koľko si vyfarbil dvojíc? - Dĺžka palice
 Joonie má tri kusy palice. Prvá palica je dlhá 4 ½ metra a druhá palica je dlhá 2 ¼. Tretia palica je dlhá 3 ¾ metra. Aká je celková dĺžka palice?
Joonie má tri kusy palice. Prvá palica je dlhá 4 ½ metra a druhá palica je dlhá 2 ¼. Tretia palica je dlhá 3 ¾ metra. Aká je celková dĺžka palice? - Paličky - trojuholník
 Boulder Bob má veľa palíc s dĺžkou 3,5 a 7. Chce tvoriť trojuholníky, z ktorých každý okraj pozostáva práve z jednej palice. Koľko nezhodných trojuholníkov možno vytvoriť pomocou tyčiniek?
Boulder Bob má veľa palíc s dĺžkou 3,5 a 7. Chce tvoriť trojuholníky, z ktorých každý okraj pozostáva práve z jednej palice. Koľko nezhodných trojuholníkov možno vytvoriť pomocou tyčiniek? - Číslo
 Ktoré číslo má tú vlastnosť, že ak odčítame od jeho päťnásobku zväčšeného o 5 jeho trojnásobok zmenšený o 3, dostaneme opäť pôvodné číslo ?
Ktoré číslo má tú vlastnosť, že ak odčítame od jeho päťnásobku zväčšeného o 5 jeho trojnásobok zmenšený o 3, dostaneme opäť pôvodné číslo ? - Myslím si číslo
 Myslím si číslo. Keď k nemu pripočítam 980 a odpočítam 416, dostanem číslo, ktoré je o 14 väčšie ako 1241. Ktoré číslo som si myslel?
Myslím si číslo. Keď k nemu pripočítam 980 a odpočítam 416, dostanem číslo, ktoré je o 14 väčšie ako 1241. Ktoré číslo som si myslel? - Z7–I–1 MO 2017
 Peter povedal Pavlovi: ”Napíš dvojciferné prirodzené číslo, ktoré má tú vlastnosť, že keď od neho odčítaš dvojciferné prirodzené číslo s tými istými ciframi napísanými v opačnom poradí, dostaneš rozdiel 63.“ Ktoré číslo mohol Pavol napísať? Určte všetky m
Peter povedal Pavlovi: ”Napíš dvojciferné prirodzené číslo, ktoré má tú vlastnosť, že keď od neho odčítaš dvojciferné prirodzené číslo s tými istými ciframi napísanými v opačnom poradí, dostaneš rozdiel 63.“ Ktoré číslo mohol Pavol napísať? Určte všetky m
