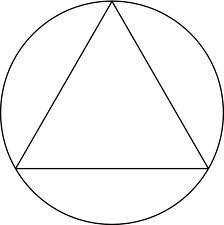
Equilateral triangle
How long should the minimum radius of the circular plate be cut into an equilateral triangle with side 21 cm from it?
Correct answer:
Tips for related online calculators
Calculation of an equilateral triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
planimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Strip
From 3 cm wide strip should be cut rhombus with area 16 cm². How long will it be on its side? - Waste
How much of the waste is from a circular plate with a radius of 1 m, from which we cut a square with the highest area? - Eq triangle minus arcs
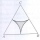In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu - Paper box
The hard rectangular paper has dimensions of 60 cm and 28 cm. We cut off the corners into equal squares, and the residue was bent to form an open box. How long must the largest volume of the box be beside the squares?
- Triangles
Hanka cut the 20 cm long straws into three pieces. Each piece had a length in cm. Then, with these three pieces, she tried to make a triangle. a) What circuit has each of the triangles? b) How long can the longest side measure? c) How many different trian - Circular sector
I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector? - Identical 3518
The carpenter cut two identical pieces into shelves from a 2-meter longboard. He cut the rest into four side shelves of 20 cm. How long are the shelves?
