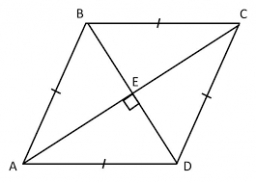
Diagonals of a rhombus 2
One diagonal of a rhombus is greater than the other by 4 cm. If the area of the rhombus is 96 cm2, find the side of the rhombus.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Diamond
Find the side of the diamond if its area is S = 194 cm² and one diagonal u2 = 44 cm. - The area 5
The area of a rhombus is 144 sq cm. If one of the diagonals is double the other, find the length of the diagonals. - One side 2
One side of the rectangle is three times larger, and the other is 4 cm smaller than the side of the square. Find the area of the square if more than the area of the rectangle by 10 cm². - Diagonals
The diagonal of a rhombus is 20 cm long. If its side is 26 cm, find the length of the other diagonal.
- Equilateral 4486
If we increase one side of the triangle by 11 cm and reduce the other by 11 cm, we get an equilateral triangle. Four times the shortest side of the triangle is 10 cm greater than three times the triangle's longest side. Find all the lengths of the sides o - The rhombus (a,d)
Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm. - Diagonals of a rhombus
One of the diagonals of a rhombus is twice the other. If the sum of the lengths of the diagonals is 24, find the area of the rhombus.
