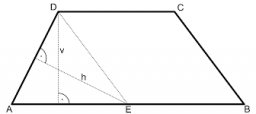
Children playground

The playground has the shape of a trapezoid, the parallel sides have a length of 36 m and 21 m, the remaining two sides are 14 m long and 16 m long. Determine the size of the inner trapezoid angles.

Result

A =  53.576 °
B =  66.868 °
C =  113.132 °
D =  126.424 °

Solution:

Solution in text A =
Solution in text B =
Solution in text C =
Solution in text D =

Try calculation via our triangle calculator.


Try another example






Leave us a comment of this math problem and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




To solve this verbal math problem are needed these knowledge from mathematics:

See also our right triangle calculator. Cosine rule uses trigonometric SAS triangle calculator. See also our trigonometric triangle calculator.

Next similar math problems:

  1. Trapezoid - RR
    right_trapezium Find the area of the right angled trapezoid ABCD with the right angle at the A vertex; a = 3 dm b = 5 dm c = 6 dm d = 4 dm
  2. Four sides of trapezoid
    lichobeznik-stredni_pricka_3 In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles.
  3. A kite
    kite2 ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC and angle BAD.
  4. Largest angle of the triangle
    obtuse_triangle Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a
  5. Greatest angle
    triangles_4 Calculate the greatest triangle angle with sides 197, 208, 299.
  6. ABCD
    trig_1 AC= 40cm , angle DAB=38 , angle DCB=58 , angle DBC=90 , DB is perpendicular on AC , find BD and AD
  7. Side c
    trig-cos-law In △ABC a=2, b=4 and ∠C=100°. Calculate length of the side c.
  8. Scalene triangle
    triangles_1 Solve the triangle: A = 50°, b = 13, c = 6
  9. Mast shadow
    horizons Mast has 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 15°. Determine the height of the mast, if the sun above the horizon is at angle 33°. Use the law of sines.
  10. Inner angles
    triangle_1111 The inner angles of the triangle are 30°, 45° and 105° and its longest side is 10 cm. Calculate the length of the shortest side, write the result in cm up to two decimal places.
  11. Medians of isosceles triangle
    iso1 The isosceles triangle has a base ABC |AB| = 16 cm and 10 cm long arm. What are the length of medians?
  12. Theorem prove
    thales_1 We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption we started?
  13. The pond
    rybnik_3 We can see the pond at an angle 65°37'. Its end points are 155 m and 177 m away from the observer. What is the width of the pond?
  14. Angles by cosine law
    357_triangle Calculate the size of the angles of the triangle ABC, if it is given by: a = 3 cm; b = 5 cm; c = 7 cm (use the sine and cosine theorem).
  15. Laws
    pyt_triangle From which law follows directly the validity of Pythagoras' theorem in the right triangle? ?
  16. Steeple
    church_tower Steeple seen from the road at an angle of 75°. When we zoom out to 25 meters, it is seen at an angle of 20°. What is high?
  17. Height 2
    1unilateral_triangle Calculate the height of the equilateral triangle with side 38.