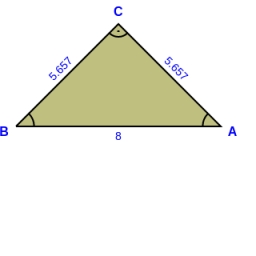
Isosceles triangle
In an isosceles triangle, the arm's length and the length of the base are in a ratio of 3 to 5. What is the length of the arm?
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Do you have a system of equations and are looking for calculator system of linear equations?
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you have a system of equations and are looking for calculator system of linear equations?
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- system of equations
- expression of a variable from the formula
- planimetrics
- perimeter
- triangle
- basic functions
- ratio
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Base of an isosceles triangle
Calculate the size of the base of an isosceles triangle; the height is 5 cm, and the arm's length is 6.5 cm. What is the perimeter of this triangle? - Isosceles triangle
What are the angles of an isosceles triangle ABC if its base is long a=5 m and has an arm b=4 m? - Height—the 6183
In the isosceles trapezoid ABCD, the base length is a = 10cm, c = 6cm, and the arm's length is 4cm. Calculate its height—the result round to tenths. - Circumference 7065
In an isosceles triangle, the base length is equal to 75% of the arm's length. If the circumference is 22 cm, determine the area of the triangle.
- Isosceles + prism
Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm. - Isosceles triangle
Calculate the size of the interior angles and the length of the base of the isosceles triangle if the arm's length is 17 cm and the height of the base is 12 cm. - Circumference 3160
In an isosceles triangle, the base length is 75% of the arm's length. If the circumference is 22 cm, calculate the area of the triangle.
