Hyperbola equation
Find the hyperbola equation with the center of S [0; 0], passing through the points:
A [5; 3] B [8; -10]
A [5; 3] B [8; -10]
Correct answer:
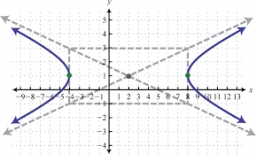
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The tangent of the hyperbola
 Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Equation - inverse
 Solve for x: 7: x = 14:1000
Solve for x: 7: x = 14:1000 - Hyperbola
 Find the equation of hyperbola that passes through the point M [30; 24] and has focal points at F1 [0; 4 sqrt 6], F2 [0; -4 sqrt 6].
Find the equation of hyperbola that passes through the point M [30; 24] and has focal points at F1 [0; 4 sqrt 6], F2 [0; -4 sqrt 6].
