Prism 4 sides
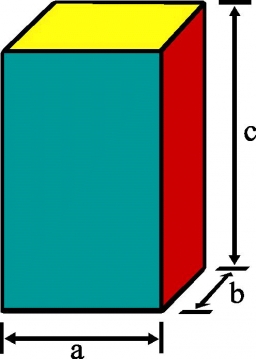
Find the surface area and volume of a four-sided prism high 10 cm if its base is a rectangle measuring 8 cm and 1.2 dm.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Four-sided prism
Find the surface area and volume of a four-sided prism high 10cm if its base is a rectangle measuring 6cm and 1.4dm. - Surface area
Calculate the surface area of a four-sided 2-m high prism whose base is a rectangle with sides of 17 cm and 1.3 dm. - Regular prism
The regular four-sided prism has a base of 25 cm² and a surface of 210 cm². Find its volume. - Triangular prism
Calculate the surface area and volume of a three-sided prism with a base of a right-angled triangle if its sides are a = 3 cm, b = 4 cm, c = 5 cm, and the height of the prism is v = 12 cm. - Equilateral 82136
A three-sided prism with a base in the shape of an equilateral triangle has a volume of 370 dm³. What is the volume of its base if it is 50 cm high? - Calculate
Calculate the surface of a regular eleven-sided prism; if the area of its base is 58 cm2, the edge of the base is 6cm long, and the height of the prism is 21 cm. - Right-angled 4951
Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5
