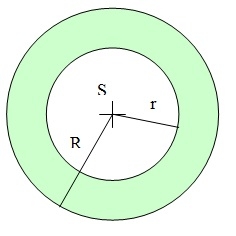
Concentric circles
There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area?
Correct answer:
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - A rectangle 13
 A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide?
A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide? - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning. - The bedroom
 The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
- Nisha
 Nisha likes to make small rectangular paintings of cats. One of her paintings has an area of 33cm squared and a width of 7 1/2 centimeters. What is the height of this painting?
Nisha likes to make small rectangular paintings of cats. One of her paintings has an area of 33cm squared and a width of 7 1/2 centimeters. What is the height of this painting? - An orange
 An orange Grove has 858 trees. There are 33 rows, each with the same number of trees. How many trees are in each row
An orange Grove has 858 trees. There are 33 rows, each with the same number of trees. How many trees are in each row - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Apothem
 Find the ratio between the two perimeters, the two areas, and two corresponding apothems of two regular hexagons whose sides are 2-3/4 inches and 4-1/8 inches.
Find the ratio between the two perimeters, the two areas, and two corresponding apothems of two regular hexagons whose sides are 2-3/4 inches and 4-1/8 inches. - Edmond 2
 Edmond bought a new cage for his pet rabbit since he's gotten so big. The area of the old cage's floor was 6 square feet. The area of the new cage's floor is n square feet larger, for a total of 8 square feet. Write expressions that tell this story and fi
Edmond bought a new cage for his pet rabbit since he's gotten so big. The area of the old cage's floor was 6 square feet. The area of the new cage's floor is n square feet larger, for a total of 8 square feet. Write expressions that tell this story and fi
- A sticky
 A sticky note shaped like a rectangle has an area of 72 square centimeters. It has a width of 8 centimeters. How long is the sticky note?
A sticky note shaped like a rectangle has an area of 72 square centimeters. It has a width of 8 centimeters. How long is the sticky note? - A triangle 9
 A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base?
A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base? - Rectangle - general expression
 Find the area of a rectangle whose width is x-2 units and length of x+4 units.
Find the area of a rectangle whose width is x-2 units and length of x+4 units. - Polynomial rectangle
 If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle.
If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle. - Jason 2
 Jason built a rectangular tool shed that is 888 meters wide and has an area of 969696 square meters. What is the length of Jason's tool shed?
Jason built a rectangular tool shed that is 888 meters wide and has an area of 969696 square meters. What is the length of Jason's tool shed?
- Native plants
 In a garden, 5/6 of the area is filled with native plants. The native plants take up 107/4 m². Let g represent the total area of the garden. Find g = total area of the garden.
In a garden, 5/6 of the area is filled with native plants. The native plants take up 107/4 m². Let g represent the total area of the garden. Find g = total area of the garden. - Poured liquid
 If I pour 59ml of liquid into an area of 594 sq mm, how thick would the liquid be?
If I pour 59ml of liquid into an area of 594 sq mm, how thick would the liquid be? - A sandbox
 3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox?
3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox?
