Pythagorean theorem - practice problems - page 3 of 73
Number of problems found: 1452
- PQR - Euclid
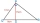 Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ.
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Trigonometric fx
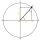 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Two points
 M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN.
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN. - Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - LS and y-axis intersection
 In what ratio is the line segment joining P (5, 3) and Q (–5, 3) divided by the y-axis? Also, find the coordinates of the intersection point.
In what ratio is the line segment joining P (5, 3) and Q (–5, 3) divided by the y-axis? Also, find the coordinates of the intersection point. - Triangle 82
 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - The coordinates 3
 The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex?
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Line segment
 Find the length of the line joining points A(-4,8) and B(-1,4).
Find the length of the line joining points A(-4,8) and B(-1,4). - The vertices
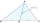 The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C.
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - Cuboid - sum of edges length
 Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - A frustum
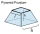 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Slant height 3
 The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height.
The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height. - Square
 Calculate the side of a square with a diagonal measurement of 10 cm.
Calculate the side of a square with a diagonal measurement of 10 cm. - Triangle
 Can an equilateral triangle have a right angle?
Can an equilateral triangle have a right angle? - Perpendicular sides
 In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle.
In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle. - RT and circles
 Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=26.
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=26. - Laws
 From which law directly follows the validity of Pythagoras' theorem in the right triangle? ...
From which law directly follows the validity of Pythagoras' theorem in the right triangle? ... - Euclid2
 The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle.
The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle. - Square
 Calculate the area of the square with diagonal 17 cm.
Calculate the area of the square with diagonal 17 cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
