Angle practice problems - page 54 of 64
Number of problems found: 1262
- Pentagonal prism
 The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism.
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism. - Block
 Calculate the volume of a cuboid ABCDEFGH if |AB| = 7 cm, |BC| = 8 cm and the angle ∠CDG = 30.1°
Calculate the volume of a cuboid ABCDEFGH if |AB| = 7 cm, |BC| = 8 cm and the angle ∠CDG = 30.1° - Carousel for children
 There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m?
There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m? - Quadrilateral prism
 Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base. - Tetrahedral pyramid 8
 Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h=
Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - Inscribed triangle
 A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle.
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Octagonal tank
 The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness.
The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness. - Tangents to ellipse
 Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1]. - Corresponding 6021
 How much paint do we need to paint a pool in the shape of a 6-sided prism? The base edge measures 21 dm, the corresponding height is 1.8 m, and the pool height is 150 cm. We need 0.21 kg of paint per 1 m².
How much paint do we need to paint a pool in the shape of a 6-sided prism? The base edge measures 21 dm, the corresponding height is 1.8 m, and the pool height is 150 cm. We need 0.21 kg of paint per 1 m². - Rhomboid
 Calculate the circumference and area of the rhomboid with sides 19 and 20, with their angle 40°.
Calculate the circumference and area of the rhomboid with sides 19 and 20, with their angle 40°. - Hexagonal prism
 The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double)
The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double) - Clock face
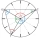 On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Shooter
 The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot?
The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot? - The mast
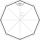 A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance.
A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance. - Hexagonal prism 2
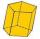 The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume.
The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume. - Common chord
 The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Trapezoid - construction
 Construct a trapezoid KLMN, where: k = 9 cm, l = 4 cm, m = 5 cm and angle α = 45°
Construct a trapezoid KLMN, where: k = 9 cm, l = 4 cm, m = 5 cm and angle α = 45° - Earth's circumference
 Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes.
Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
