The mast
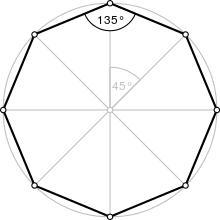
A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance.
Final Answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Position 19113
 The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po
The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po - Antenna mast
 The antenna mast is 26 meters high. It is fixed by four steel cables suspended 1.6 meters below the highest point of the mast and anchored to the ground at the vertices of a square with a side length of 14 meters. The mast is erected in the center of this
The antenna mast is 26 meters high. It is fixed by four steel cables suspended 1.6 meters below the highest point of the mast and anchored to the ground at the vertices of a square with a side length of 14 meters. The mast is erected in the center of this - Distance 79874
 The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed?
The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed? - Oil rig
 The oil drilling rig is 23 meters in height and fixes the ropes, the ends of which are 10 meters away from the foot of the tower. How long are these ropes?
The oil drilling rig is 23 meters in height and fixes the ropes, the ends of which are 10 meters away from the foot of the tower. How long are these ropes? - Transmitter 34201
 A television transmitter 108 m high is anchored at 2/3 of its height (from the ground) by three ropes of equal length. How many meters of rope are needed for anchoring if it is embedded at a distance of 54 m from the foot of the mast, and we count 10% of
A television transmitter 108 m high is anchored at 2/3 of its height (from the ground) by three ropes of equal length. How many meters of rope are needed for anchoring if it is embedded at a distance of 54 m from the foot of the mast, and we count 10% of - Voltage 2533
 The high voltage mast fastens 30 m long ropes at 2/3 of the mast height. How tall is the mast if the ropes anchor at 15 m from the mast?
The high voltage mast fastens 30 m long ropes at 2/3 of the mast height. How tall is the mast if the ropes anchor at 15 m from the mast? - Simultaneously 5610
 Two cyclists rode towards each other simultaneously from opposite ends of the 28km long route. Each covered the entire route at a constant speed, the fastest being at the finish line 35 minutes earlier. On the route, the cyclists passed each other after 1
Two cyclists rode towards each other simultaneously from opposite ends of the 28km long route. Each covered the entire route at a constant speed, the fastest being at the finish line 35 minutes earlier. On the route, the cyclists passed each other after 1
