Angle practice problems - page 53 of 63
Number of problems found: 1258
- Right angled triangle 2
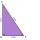LMN is a right-angled triangle with vertices at L(1,3), M(3,5), and N(6,n). Given angle LMN is 90° find n - Glass
How many glasses are needed to produce glass with a base of a regular 5-gon if one base triangle in the base is 4.2 square cm and the height is 10 cm? - Parallelogram - area
Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°. - Quadrilaterals II
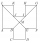In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M and divide the dodecago - Black building
Jozef built building with a rectangular shape 3.9 m × 6.7 m. Calculate how much percent exceeded the limit 25 m² for a small building. A building not built by the law is called a "black building". Calculate the angle that the walls were clenching each oth - Rectangular trapezoid
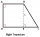The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Trapezoid - construction
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Track arc
Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - Octagonal pyramid
Find the volume of a regular octagonal pyramid with height v = 100 and the angle of the side edge with the base plane is α = 60°. - Rhombus IV
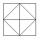Calculate the length of the diagonals of the rhombus, whose sizes are in the ratio of 1:2 and a rhombus side is 35 cm. - Constructed 77874
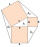Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same. - Construction 6411
Draw an isosceles trapezoid ABDC if a = 6cm, v = 5cm, beta = 60 degrees. / sketch, procedure, construction / - Diagonals at right angle
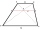In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Octagon
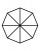We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon? - 30-gon
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Equilateral triangle
How long should the minimum radius of the circular plate be cut into an equilateral triangle with side 21 cm from it? - Rhombus
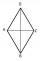ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus. - Hexagon area
The center of the regular hexagon is 21 cm away from its side. Calculate the hexagon side and its area. - Octagon from rectangle We cut the corners of a rectangular tablecloth with dimensions of 4 dm and 8 dm into isosceles triangles. Thus, the octagon formed had an area of 26 dm². How many dm² of tablecloth do we cut down?
- Hexagon - MO
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ|
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
