Area of Trapezoid Problems - page 8 of 10
Number of problems found: 187
- Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Isosceles trapezoid
In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm². - Divide an isosceles triangle
How can an isosceles triangle be divided into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)? - Length 26
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Trapezoid perimeter calculation
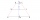Find the points A1 B1 symmetric along the y-axis to the points A [-4,0] and B [-1,4]. Calculate the perimeter of the trapezoid AB B1 A1. - Trapezoid proof
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Trapezoid IV
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD? - Four sides of trapezoid The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
- Temperature and volume
The pool with a length of l = 50 m and a width of s = 15 m has a depth of h1 = 1.2 m at the shallowest part of the wall. The depth then gradually increases to a depth of h2 = 1.5 m in the middle of the pool. = 4.5 m walls in the deepest part of the pool. - Four prisms
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t - Pit
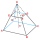The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n - Wooden 3
A wooden board 2.5 m long has a cross-section in the shape of a regular trapezoid whose parallel sides have lengths of 1.2 dm and 8 cm. The height of the trapezoid is 3 cm. Calculate: a) the surface area of the board to calculate the consumption of stai - Pillar - bricks
A brick pillar has the shape of a four-sided prism with an isosceles trapezoid base with sides a = 55 cm, c = 33 cm, side b = 33 cm, height of the trapezoid va = 32.1 cm. The pillar is 1.9 m high. How many bricks were used to build it if one brick has a v - Base RR odd
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Groundwater
The groundwater for collecting rainwater has the shape of a prism with trapezoidal bases a=5 m, c=7 m, 4 meters apart. The depth of the tank is 3 meters. How many hectoliters of water can it hold at most if 8% of its volume is taken up by the pump and pip - Aquarium height
The aquarium has the shape of a prism with a trapezoidal base. The length of the basic trapezoid is 60 cm and 80 cm, and the height of the trapezoid is 70 cm. The aquarium holds 196 liters of water. How tall is the aquarium? - Cross-section - digging
How many m³ of soil is to be excavated when digging a 120 m long ditch, the cross-section of which is an isosceles trapezoid with bases of 2.3 m and 3.3 m, if the depth of the trench is 90 cm? - Cross-section of a roof
The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
