Area of Triangle Problems - page 22 of 42
Number of problems found: 837
- Cross-section - trapezoid
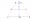 The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width.
The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width. - MO Z8–I–6 2018
 The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line.
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Park
 Rotating sprayer irrigation lawns will permanently surround the newly built park. Find the largest radius of the circle that can be irrigated by sprayer P, not to spray park visitors online AB. Distance AB = 55 m, AP = 36 m and BP = 28 m.
Rotating sprayer irrigation lawns will permanently surround the newly built park. Find the largest radius of the circle that can be irrigated by sprayer P, not to spray park visitors online AB. Distance AB = 55 m, AP = 36 m and BP = 28 m. - Archaeologists 81478
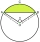 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Consumption 69174
 The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste.
The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste. - The farmer
 The farmer would like to first seed his small field. The required amount depends on the seed area. The field has a triangular shape. The farmer had a fenced field, so he knew the lengths of the sides: 73, 117, and 63 meters. Find a suitable way to determi
The farmer would like to first seed his small field. The required amount depends on the seed area. The field has a triangular shape. The farmer had a fenced field, so he knew the lengths of the sides: 73, 117, and 63 meters. Find a suitable way to determi - Center of gravity
 In the isosceles triangle ABC the lengths of AB and the height to AB is the ratio of 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT.
In the isosceles triangle ABC the lengths of AB and the height to AB is the ratio of 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT. - Measurements of a triangle
 Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft - ISO triangle
 Calculate the area of an isosceles triangle KLM if its sides' length is in the ratio k:l:m = 4:4:3 and has a perimeter 352 mm.
Calculate the area of an isosceles triangle KLM if its sides' length is in the ratio k:l:m = 4:4:3 and has a perimeter 352 mm. - Isosceles 5711
 An isosceles triangle with a base length of 32 cm has an area of 480 cm². What's his perimeter?
An isosceles triangle with a base length of 32 cm has an area of 480 cm². What's his perimeter? - Dipole - complex power
 For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice.
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice. - Eq triangle minus arcs
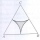 In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu
In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu - Rhombus and diagonals
 The rhombus area is 150 cm2, and the ratio of the diagonals is 3:4. Calculate the length of its height.
The rhombus area is 150 cm2, and the ratio of the diagonals is 3:4. Calculate the length of its height. - Circumference 3160
 In an isosceles triangle, the base length is 75% of the arm's length. If the circumference is 22 cm, calculate the area of the triangle.
In an isosceles triangle, the base length is 75% of the arm's length. If the circumference is 22 cm, calculate the area of the triangle. - Right-angled 81359
 The paths in the park form a right-angled triangle, which on the map with a scale of 1:200 has two dimensions of side lengths of 9cm and 15cm. Grandma walks this route every day for a health walk. How many meters does she walk?
The paths in the park form a right-angled triangle, which on the map with a scale of 1:200 has two dimensions of side lengths of 9cm and 15cm. Grandma walks this route every day for a health walk. How many meters does she walk? - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - Calculate
 Two friends Mário and Jano lived on two different sides of a highway. They decided to find out how wide it was. Mário drew a picture, based on which they then made measurements the next day. They measured the values a =5m, b= 5.9 m, and d = 5 m. Calcula
Two friends Mário and Jano lived on two different sides of a highway. They decided to find out how wide it was. Mário drew a picture, based on which they then made measurements the next day. They measured the values a =5m, b= 5.9 m, and d = 5 m. Calcula - Squares above sides
 Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu - Kite
 John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper does John need to make a kite if he needs paper on both sides and needs 5% of the paper for bending?
John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper does John need to make a kite if he needs paper on both sides and needs 5% of the paper for bending? - Airport's 80482
 The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm?
The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
