Basic operations and concepts - math word problems - page 185 of 321
Number of problems found: 6419
- Lawn and garden
The garden around the new house is divided as follows: 30% flowers, 35% orchards, and 150 m² form a lawn. What is the total area of the garden? - Quatrefoil 81138
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters. - Reconstruction 23531
The enclosure for lions in the ZOO has a rectangular shape with a length of 5.6m and a width of 6.8m. During the reconstruction, the length of the fence must be adjusted to 5.2 m so that the size (areas) of the paddock stays the same. What will be the wid - Rectangular 6397
Calculate the area of Mr. Vejvoda's rectangular garden rounded to whole hectares if you know that garden fencing, including gates and doors, is 420 m long and its dimensions are in the ratio of 9:5 - Circumference 6382
Jan bought a large rectangle plot with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of the same length. Their longer sides are three consecutive natural numbers. Find out each plot's dimens - The angles
The angles in the triangle are in the ratio 12:15:9. Find the angles. - Identical line
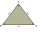In which triangles is the line identical with the height? - Circumference of the garden
The garden is 90 m long. What is the smallest width if it is possible to walk (circumference) in steps of 80 cm or 50 cm? - Property
The length of the rectangle-shaped property is 8 meters, less than three times the width. If we increase the width by 5% of the length and the length by 14% of the width, the property perimeter will increase by 13 meters. How much will the property cost p - BW-BS balls
Adam has a full box of large or small balls, black or white. The ratio between large and small balls is 5:3. Within the large balls, the ratio of black to white is 1:2, and between small balls, the ratio of black to white is 1:8. What is the ratio of all- - Percentage 3980
Calculate the percentage of waste when we cut out 4 of the largest possible circles from a square sheet with sides of 1 meter. - Carpet
The room is 10 x 5 meters. You have the role of carpet width of 1 meter. Make a rectangular cut of a roll. That piece of carpet will be the longest possible and will fit into the room. How long is a piece of carpet? Note: The carpet will not be parallel w - Rectangle
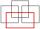The perimeter of the rectangle is 22 cm, and the area is 30 cm². Determine its dimensions if integers express the length of the sides of the rectangle in centimeters. - Wheat
The rectangle-shaped field with dimensions 529 m and 1001 m harvested last year was 2780 q wheat. (1 q = 1 quintal = 100 kg). During the year, it was necessary to fix the pipe and therefore did kick wide 4 m parallel to the side of the field 1001 m, were - The circumference
The circumference and width of the rectangle are in a ratio of 5:1. Its area is 216 cm². What is its length? - Rectangular garden The perimeter of Peter's rectangular garden is 98 meters. The width of the garden is 60% shorter than its length. Find the dimensions of the rectangular garden in meters. Find the garden area in square meters.
- Triangle
Can an equilateral triangle have a right angle? - Transmitter 34201
A television transmitter 108 m high is anchored at 2/3 of its height (from the ground) by three ropes of equal length. How many meters of rope are needed for anchoring if it is embedded at a distance of 54 m from the foot of the mast, and we count 10% of - Square - increase sides
If we increase the length of one pair of opposite sides of the square by 2 cm and the length of the other two sides by 1 cm, we will create a rectangle, the perimeter of which will be 10% larger than the perimeter of the original square. What is the side - The carpet
How many meters of carpet 90 cm wide need to cover the floor room, which has a rectangular shape with lengths of 4.8 m and 2.4 m, if the number of pieces on the carpet is needed to be lowest?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
