Right triangle - ratio
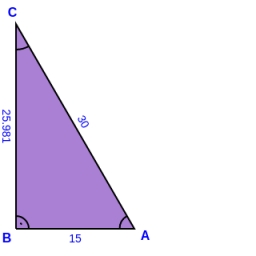
The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle.
Your answer:
Your answer:
Tips for related online calculators
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetrybasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Right-angled - legs
The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c - Median in right triangle
In the rectangular triangle, ABC has known the length of the legs a = 15 cm and b = 36 cm. Calculate the length of the median to side c (to hypotenuse). - Triangle height ratio
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Right triangle ABC
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - Legs and ratio
The legs of a right triangle are in the ratio a:b = 6:8. The hypotenuse has a length of 61 cm. Calculate the perimeter and area of this triangle. - Rectangular triangles
The lengths of the corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and - Right triangle
The legs of a right triangle are in the ratio a:b = 2:8. The hypotenuse has a length of 87 cm. Calculate the perimeter and area of the triangle.
