Circle practice problems - page 40 of 50
Number of problems found: 992
- Calculate 3562
 The 16 cm long string is 6 cm from the circle's center. Calculate the length of the circle.
The 16 cm long string is 6 cm from the circle's center. Calculate the length of the circle. - Given is
 Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle.
Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle. - Ratio of squares
 A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Rhombus
 It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Tangent 3
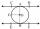 In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm.
In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm. - Annulus from triangle
 Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm.
Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm. - The fence
 I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The
I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The - Track arc
 Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)?
Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - 30-gon
 The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Rhombus and inscribed circle
 It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals.
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Sidewalk
 The city park is a circular bed of flowers with a diameter of 8 meters. Around it, the whole length is 1-meter wide sidewalk. What is the sidewalk area?
The city park is a circular bed of flowers with a diameter of 8 meters. Around it, the whole length is 1-meter wide sidewalk. What is the sidewalk area? - From plasticine
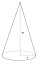 Michael modeled from plasticine a 15 cm high pyramid with a rectangular base, with the sides of the base a = 12 cm and b = 8 cm. From this pyramid, Janka modeled a rotating cone with a base diameter of 10 cm. How tall was Janka's cone?
Michael modeled from plasticine a 15 cm high pyramid with a rectangular base, with the sides of the base a = 12 cm and b = 8 cm. From this pyramid, Janka modeled a rotating cone with a base diameter of 10 cm. How tall was Janka's cone? - Two chords
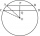 Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords.
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Quadrilateral 78874
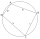 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Construct 80719
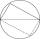 Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle.
Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle. - 2d shape
 Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm.
Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm. - Two parallel chords
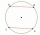 The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle.
The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle. - Two chords
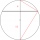 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Park
 Rotating sprayer irrigation lawns will permanently surround the newly built park. Find the largest radius of the circle that can be irrigated by sprayer P, not to spray park visitors online AB. Distance AB = 55 m, AP = 36 m and BP = 28 m.
Rotating sprayer irrigation lawns will permanently surround the newly built park. Find the largest radius of the circle that can be irrigated by sprayer P, not to spray park visitors online AB. Distance AB = 55 m, AP = 36 m and BP = 28 m. - Pentagonal prism
 The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism.
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
