Combinatorics - math word problems - page 23 of 54
Number of problems found: 1080
- Socks
Ben's favorite colors are blue and green. He has six blue socks and six green socks in his sock drawer. Unfortunately, they are completely mixed up, and one day, he has to grab some socks to wear in complete darkness. How many socks (minimum) does he have - Sum or product
What is the probability that two dice fall will have the sum of seven or product 12? - Seven-segmet
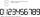Lenka is amused that he punched a calculator (seven-segment display) number and used only digits 2 to 9. Some numbers have the property that She again gave their image in the axial or central symmetry some number. Determine the maximum number of three-dig - Word OPTICAL
Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together. - Desks
A class has 20 students. The classroom consists of 20 desks, with four desks in each of 5 different rows. Amy, Bob, Chloe, and David are all friends and would like to sit in the same row. How many possible seating arrangements exist, such as Amy, Bob, Chl - Left-handed writer
Eva, Lucia, Barbora, Ivana, and Slávka are good friends, so they always want to sit at one long table next to each other in biology class. How many ways can they sit if Slavka is left-handed and, therefore, always wants to sit on the left side of the tabl - Competition 67314
The coach must choose two students from Sam, Jura, Emma, Dan, and Nika to go to the competition. He knows them well and knows that Samo will only go with Jura or Ema, and Dano will not go with Ema. How many pairs does the trainer have to choose from? - Ornamental 6532
The gardener is to plant 6 ornamental trees. There are 8 different types of trees available. Two trees, A and B, will be planted on the left edge. How many ways can a gardener do this if all the saplings planted are to be different? - Two doctors
Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient. - Family trip
Dulikovci, Elikovci, Filikovci, and Galikovci visited each other often last month. Each family visited each family exactly once. How many visits did all four families make together? If two families came to visit one family simultaneously, count it twice. - Possibilities 66804
Without listing all the possibilities, calculate how many different pairs can be made A) of 12 pupils who want to go down a water slide on a two-seater inflatable in the water park. B) of 15 pupils who want to ride toy cars in the amusement park. - Tournament 4771
Eight tennis players took part in the tennis tournament. They were divided into two groups of four. In each group, everyone played each other once. The winner of the first group played the winner of the second group in the final. They did not play other m - Wedding guests
Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs. - Password
The voltage station is day changing the master password, which consists of three letters. The code generation process does not change and is based on the following procedure: The following letters (A) to (I) correspond to different numbers from 1 to 9 if - Twelve flowers
A florist has roses, tulips, daffodils, and carnations to use in flower arrangements. If she were to make an arrangement using 12 flowers, how many different combinations of these four types of flowers would be possible? - Complexity 30631
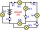Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here. A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the - Phone numbers
How many 9-digit telephone numbers can be compiled from the digits 0,1,2,..,8,9 that no digit is repeated? - Numbered
In the past, passengers in public transport vehicles marked such single-use tickets, which had 9 numbered boxes, a certain number of which were punched with a marker. A) In how many different ways could the ticket be marked if 3 boxes were punched? B) How - Light bulbs
You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb - Cinema
How many ways can 11 free tickets to the premiere of "Jáchyme throw it in the machine" be divided between 6 pensioners?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
