Diagonal + right triangle - practice problems - page 11 of 18
Number of problems found: 355
- Diagonals
 Draw a square ABCD whose diagonals have a length of 6 cm.
Draw a square ABCD whose diagonals have a length of 6 cm. - Construct
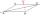 Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long.
Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long. - Diagonal of the diamond
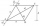 The ABCD diamond shape is known as diagonal u2 and a height v. Do an analysis.
The ABCD diamond shape is known as diagonal u2 and a height v. Do an analysis. - Construct 5868
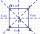 Construct a square if u-a = 1
Construct a square if u-a = 1 - Billiard balls
 A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. - Diagonals 3580
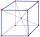 Cube edge length 5cm. Draw different diagonals.
Cube edge length 5cm. Draw different diagonals. - Prism + rhomboid
 The prism-shaped vessel with a rhomboid base has one base diagonal of 10 cm and the edge of the base 14 cm. The edge of the base and the prism height are in a ratio of 2:5. How many liters of water is in the container when it is filled to four-fifths of t
The prism-shaped vessel with a rhomboid base has one base diagonal of 10 cm and the edge of the base 14 cm. The edge of the base and the prism height are in a ratio of 2:5. How many liters of water is in the container when it is filled to four-fifths of t - Last storm - tree
 Mr. Radomír had a misfortune during the last storm; a tree fell on his roof in the shape of a regular four-sided pyramid and destroyed it all. The roof has a base edge length of 8m and a side edge length of 15m. How many m² of roofing will he have to buy?
Mr. Radomír had a misfortune during the last storm; a tree fell on his roof in the shape of a regular four-sided pyramid and destroyed it all. The roof has a base edge length of 8m and a side edge length of 15m. How many m² of roofing will he have to buy? - Hexagon rotation
 A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated?
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated? - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Cubes
 One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm².
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Support colum
 Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m.
Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m. - Flowerbed
 The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl
The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl - Horizontally 8187
 We turn the prism-shaped box with a height of 1 m and a square base with an edge of 0.6 m under a force of 350 N, which acts horizontally compared to the upper edge. What is the weight of the box?
We turn the prism-shaped box with a height of 1 m and a square base with an edge of 0.6 m under a force of 350 N, which acts horizontally compared to the upper edge. What is the weight of the box? - Pyramidal 44061
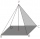 A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height?
A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height? - Faces diagonals
 Find the cuboid volume if the cuboid's diagonals are x, y, and z (wall diagonals or three faces). Solve for x=1.6, y=1.8, z=1.6
Find the cuboid volume if the cuboid's diagonals are x, y, and z (wall diagonals or three faces). Solve for x=1.6, y=1.8, z=1.6 - Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Cuboid diagonal
 Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees.
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees. - Pine wood
 We cut a carved beam from a pine trunk 6 m long and 35 cm in diameter. The beam's cross-section is in the shape of a square, which has the greatest area. Calculate the length of the sides of a square. Calculate the volume of lumber in cubic meters.
We cut a carved beam from a pine trunk 6 m long and 35 cm in diameter. The beam's cross-section is in the shape of a square, which has the greatest area. Calculate the length of the sides of a square. Calculate the volume of lumber in cubic meters. - Side wall planes
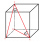 Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
