Geometry - math word problems - page 22 of 162
Number of problems found: 3238
- 3d vector component
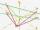The vector u = (3.9, u3), and the length of the vector u is 12. What is, is u3? - Dimension of foundations
The foundation pit for building houses has a face of blocks with dimensions of 10 meters, 10 meters, and 2 meters. After a heavy rain, the water is filled to the brim. The pump pumps out 10 m³ of water in 1 hour. In how many hours will the pit be empty? - Cylindrical tank
The tank has the shape of a rotating cylinder with a base diameter of d = 3.4 m and a height of 4.5 m. How many liters of water are in the tank if the tank is filled to 2/3? - Empty aquarium
How much does an empty aquarium weigh with dimensions: length = 40 cm, width = 30 cm, height = 20 cm, if 1 dm² of glass weighs 300 g? Calculate its weight in kilograms. - Children's pool
The children's pool at the swimming pool is 10m long, 5m wide, and 50cm deep. Calculate: (a) how many m² of tiles are needed to line the perimeter walls of the pool? (b) how many hectoliters of water will fit into the pool? - Water tank
The water tank has a cylindrical shape with a base diameter of 4.2 m and is 80 cm deep. How many minutes will it take to fill it 10 cm below the edge of the tank if water flows 2 liters per second? - Concreted
The tank of a biological treatment plant has the shape of a cylinder with a base diameter of 2.5m. It is usually filled to four-fifths of its volume. What is the volume of the treatment plant if its height is 2.8m? The treatment plant container is placed - Roof repair
To repair the roof, we need 15 pieces of boards 6 m long, 15 cm wide, and 25 mm thick. If 1 m³ of boards costs 500 euros, how many euros will we pay for all the boards? - Pool Water Height
A 1-meter-wide sidewalk will be paved around the block-shaped pool in the garden. The dimensions of the bottom of the pool are 8.5 meters and 6 meters. The height of the pool walls is 2 meters. There are 86.7 m³ of water in the pool. How high did the wate - Sand loading
The truck, with a load capacity of 7 tons, has a storage area of 4.5 m and 2.1 m. The weight of 1 m³ of wet sand is 2,000 kg. How high can we load the sand, so the car's load capacity is not exceeded? - Hemisphere - roof
The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint - Recommended dimensions
Michael bought an aquarium in the shape of a block with dimensions of the bottom 30 cm x 15 cm and a height of 20 cm. The salesman recommended that he fill the aquarium with water only up to a height of 15 cm. How many liters of water does Michael have to - Board paint calculation
Štěpán painted a block-shaped steel board measuring 2.2 m, 1.5 m, and 1.6 m twice with a protective coating. How many kilograms of paint would he consume if he used 120g of paint per 1m²? - Iron pipe weight
The iron pipe has a length of 2m and a diameter of 4cm. If the density of iron is 7870 kg/m3, calculate its weight. - Concrete box
The concrete box with walls thick 6 cm has the following external dimensions: length 1.6 m, width 39 cm, and height 32 cm. How many liters of soil can fit if I fill it to the brim? - Cans
How many m² of metal sheet is needed to produce 20,000 cans in the shape of a cylinder with a base radius and a height of 5 cm? - Three-quarters pool How many liters of water are in a cube-shaped pool with dimensions equal to 3 whole six meters b equals one full 9 meters and a depth of one total 5 meters if it is filled to only three-quarters of its volume?
- Conserving water
Calculate how many euros are spent annually on unnecessary domestic hot water, which cools during the night in the pipeline. The residential house has 223 m of hot water pipelines 1" and the hot water has a price of 14.6 Eur/m³. - Cuboid volume units
Calculate the volume of the cuboid in the given unit if you know the lengths of its edges. A) a = 20 cm, b = 3 cm, c = 7 cm, (length) B) a = 10 mm, b = 8 mm, c = 9 mm, (ml) C) a = 30 cm, b = 5 cm, c = 8 cm, (l) D) a = 300 mm, b = 4 m, c = 7 dm, (hl) - Barrel water
The cylindrical barrel is 1.2 m high, and the diameter of its base is 0.6 m. How many hectoliters of water will fit in the barrel? What is the smallest amount of sheet metal needed for its production? (we count both bases)
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
