Geometry - math word problems - page 58 of 162
Number of problems found: 3227
- Whitewashed 3483
The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas - Sphere volume formula
If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7 - Thousand balls
We must create a thousand balls from a sphere with a diameter of 1 m. What will be their radius? - The cube
The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume. - Cylinder 11141
The area of the cylinder shell is 300 cm², the height of which is equal to the diameter of the base. Find the surface of the cylinder. - Diameter 21173
The water ball has a volume of 32,500 m³. How big is its diameter? - Office
The office building was built in the shape of a regular hexagon inscribed in a circle with a radius of 12 m. The height of the walls is 7m. How much does CZK cost to plaster the building walls per 1 m square cost CZK 400?
- Giant coin
From coinage, metal was produced into giant coins and applied so much metal, such as producing 10 million actual coins. What has this giant coin's diameter and thickness if the ratio of diameter to thickness is the same as an actual coin, which has a diam - The fence
I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The - Identical 82514
What is the volume of a large cube composed of 27 identical small cubes with an edge length of 3 cm? - Created 68734
From how many cubes with a 4 cm edge can a cube with a 16 cm edge be created? - Rainwater 2770
The garden tank for rainwater is cuboid in shape, the bottom of which is square, with a side 150 cm long and 80 cm high. How many 15-liter buckets do we need to drain the water from the tank? - Cross-section of iron bar
What is the mass of an iron bar 1.5 m long, the cross-section of which is a rhombus with side a = 45 mm and a corresponding height of 40 mm? Iron density ρ = 7.8 g/cm³? What is the surface of the iron rod? - Length 83358
A block-shaped pool has a length of 50m, width of 25m, and depth of 3.5 m. When the pool is filled 50 cm below the edge, how many hectoliters of water is in it? If we paint the inside of the pool two coats and you pay 50 cents per 1m2, how much - Cube 2
How many times will increase if the surface area of the cube if we triple the length of its edge?
- The surface
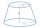The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Length of the edge
Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number. - Gasoline tank cylindrical
What is the inner diameter of the tank, which is 8 m long and contains 40 cubic meters of gasoline? - Calculate 45991
Calculate the radius of a sphere with the same volume as a cone with a radius of 5cm and a height of 7cm. - Area of a cube
Calculate the surface area of a cube if its volume is equal to 729 cubic meters.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
