Geometry - practice problems - page 4 of 162
Number of problems found: 3238
- A solid
 A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid .
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid . - Cylinders and cube
 How many cylinders of radius 20 cms and height 0.7 metres can be formed by melting a cube of 2.2 metres sides?
How many cylinders of radius 20 cms and height 0.7 metres can be formed by melting a cube of 2.2 metres sides? - A teacher 3
 A teacher gives pens and pencils to elementary students at an equal rate in each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the unknown value for the letter B.
A teacher gives pens and pencils to elementary students at an equal rate in each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the unknown value for the letter B. - A gym
 The A gym offers two packages for yearly memberships. The first plan costs $50 to be a member. Then, when you visit the gum, it is $5 to get in. The second plan costs $200, but it only costs $2 to get in each time you visit. How many visits would it take
The A gym offers two packages for yearly memberships. The first plan costs $50 to be a member. Then, when you visit the gum, it is $5 to get in. The second plan costs $200, but it only costs $2 to get in each time you visit. How many visits would it take - The midday
 The midday temperature in Pensacola Beach was 84°F. For the next five hours, it changed to –2°F per hour. The expression 84 − |−2 ⋅ 5| represents the current temperature. What is the current temperature in degrees Fahrenheit?
The midday temperature in Pensacola Beach was 84°F. For the next five hours, it changed to –2°F per hour. The expression 84 − |−2 ⋅ 5| represents the current temperature. What is the current temperature in degrees Fahrenheit? - Temperature bellow zero
 At 3 PM, the temperature was 12°F. It then began dropping 2°F every hour for 7 hours. What was the temperature after 7 hours?
At 3 PM, the temperature was 12°F. It then began dropping 2°F every hour for 7 hours. What was the temperature after 7 hours? - Y-intercept 2
 What is the y-intercept of 4x + 8y =16? Write coordinates of x0, y0 of that y-intercept.
What is the y-intercept of 4x + 8y =16? Write coordinates of x0, y0 of that y-intercept. - Slope of line
 What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)?
What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)? - A 100-inch
 A 100-inch stick is to be divided into four using the ratio 2: 5: 7: 11. How long is the longest piece?
A 100-inch stick is to be divided into four using the ratio 2: 5: 7: 11. How long is the longest piece? - Jane and tent
 Jane and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then,
Jane and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then, - Three cubes
 Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube.
Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube. - New drink
 Create a new drink can that will double the volume of the original can used. The dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : O
Create a new drink can that will double the volume of the original can used. The dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : O - Spheres to cone
 Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed. - Melting 3 cubes
 The sides of the three metal cubes are 30 cm, 40 cm, and 50 cm, respectively. Find the side of the new cube formed by melting these cubes together.
The sides of the three metal cubes are 30 cm, 40 cm, and 50 cm, respectively. Find the side of the new cube formed by melting these cubes together. - Line slope
 What is the slope of the line with points (-1,-3) and (-5, 2)?
What is the slope of the line with points (-1,-3) and (-5, 2)? - A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - Geometric Solid
 A concrete pipe is 1.0 m long. The inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (in cubic meters) needed to make 25 pieces of pipe?
A concrete pipe is 1.0 m long. The inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (in cubic meters) needed to make 25 pieces of pipe? - Saria
 Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box?
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Storage shed
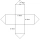 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
