Goniometry and trigonometry - math word problems - page 23 of 32
Number of problems found: 624
- Road drop
A 12 percent drop is marked on a straight stretch of road. What angle aligns the direction of the road with the horizontal plane? - Angle between lines
Calculate the angle between these two lines: p: -4x +7y +7 =0 q: -x +4y +7=0 - Difference - altitude
The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter? - The tower
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - Goat
The meadow is a circle with a radius r = 19 m. How long must a rope tie a goat to the pin on the meadow's perimeter to allow the goat to eat half of the meadow? - Difference 6029
Between the resorts is 15km, and the climb is 13 permille. What is the height difference? - Angle of climb
At what angle does the road rise if the climb is 10%? - The angle of lines
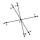Calculate the angle of two lines y=x-8 and y=+12 - Traffic sign
There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls). - Straight road
The straight road has a rise of 19%. How big is the pitch angle? - Depth angles
At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad? - Maximum area of rhombus
Calculate the interior angles at which the equilateral rhombus has a maximum area. - Chord 24
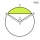A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Triangle angles
In the triangle ABC, a: b = 3:2 and α: β = 2:1. Calculate the ratio a: c. - Road
A ratio of 1:15 gives the average climb of the road. By what angle does the road moderate climb? - Wheel gear
A drive wheel of radius two is connected to a drive wheel of radius one by a pulley of length 17. What is the distance between the wheel axles? - Right triangle eq2
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70. - Perimeter - ASA theorem
Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees. - Sine theorem 2
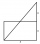From the sine theorem, find the ratio of the sides of a triangle whose angles are 30°, 60°, and 90°. - Right
Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 5a +5b = 7c
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
