Goniometry and trigonometry - math word problems - page 31 of 32
Number of problems found: 629
- Calculate sides
 In the triangle, the side length AB = 6 cm, the height to side c = 5 cm, and the angle BCA = 35°. Calculate sides a b.
In the triangle, the side length AB = 6 cm, the height to side c = 5 cm, and the angle BCA = 35°. Calculate sides a b. - Boat
 A force of 209 kg (2090 N) is required to pull a boat up a ramp inclined at 12° with horizontal. How much does the boat weigh?
A force of 209 kg (2090 N) is required to pull a boat up a ramp inclined at 12° with horizontal. How much does the boat weigh? - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Inclined plane
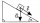 The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body.
The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body. - Vector components
 The force R = 12 N is divided into two components, F1 and F2. Their directions make angles α = 30°, β = 45° with the direction R. What are the components F1 and F2?
The force R = 12 N is divided into two components, F1 and F2. Their directions make angles α = 30°, β = 45° with the direction R. What are the components F1 and F2? - An azimuth
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started. - Motion on circle
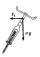 The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate.
The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Resultant force
 Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25°
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25° - Observatory and aircraft
 The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee - Inclined plane
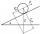 On the inclined plane with an inclination angle of 30°, we will put the body (fixed point) with mass 9 kg. Determine the acceleration of the body motion on an inclined plane.
On the inclined plane with an inclination angle of 30°, we will put the body (fixed point) with mass 9 kg. Determine the acceleration of the body motion on an inclined plane. - House roof
 The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof?
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof? - Heptagonal pyramid
 A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Cuboid diagonal
 Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees.
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees. - Parallelogram - area
 OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100°. What is its area?
OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100°. What is its area? - Square equal rhombus
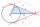 Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°.
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°. - Tropical, mild and arctic
 How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'.
How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'. - Sphere in cone
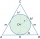 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - Regular quadrangular pyramid
 How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%.
How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%. - Big Earth
 What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
