Goniometry and trigonometry - practice problems - page 9 of 32
Number of problems found: 629
- Diagonals
 The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus.
The rhombus has two diagonals, e=14 dm, and f=11 dm. Calculate the side angle and height of the rhombus. - Maple
 The maple peak is visible from a distance of 7 m from the trunk from a height of 1.8 m at an angle of 46°. Find the height of the maple.
The maple peak is visible from a distance of 7 m from the trunk from a height of 1.8 m at an angle of 46°. Find the height of the maple. - Triangle side
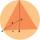 I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle.
I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle. - Dodecagon
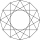 Find the area of a regular dodecagon (n=12) if the radius of the circumscribed circle is 5 cm.
Find the area of a regular dodecagon (n=12) if the radius of the circumscribed circle is 5 cm. - Right Triangle Angle
 In a right triangle ABC, the hypotenuse c = 8 cm and the side b = 4 cm. What is the size of angle α?
In a right triangle ABC, the hypotenuse c = 8 cm and the side b = 4 cm. What is the size of angle α? - Base and legs
 A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse?
A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse? - The staircase
 The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase.
The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase. - Right triangle
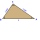 A right triangle ABC is given, and c is a hypotenuse. Find the length of the sides a, b, the angle beta if c = 5 and angle alfa = A = 35 degrees.
A right triangle ABC is given, and c is a hypotenuse. Find the length of the sides a, b, the angle beta if c = 5 and angle alfa = A = 35 degrees. - The cable car
 The cable car is 3,5 kilometers long and climbs at a 30 degrees angle. What is the altitude difference between the Upper and Lower stations?
The cable car is 3,5 kilometers long and climbs at a 30 degrees angle. What is the altitude difference between the Upper and Lower stations? - One side
 One side is 36 long with a 15° incline. What is the height at the end of that side?
One side is 36 long with a 15° incline. What is the height at the end of that side? - Ladder slope
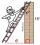 What is the slope of a ladder 6.2 m long and 5.12 m in height?
What is the slope of a ladder 6.2 m long and 5.12 m in height? - Triangle
 Calculate the area of the right triangle ΔABC if one leg is long 12 and its opposite angle is 47°.
Calculate the area of the right triangle ΔABC if one leg is long 12 and its opposite angle is 47°. - An angle
 An angle x is opposite side AB which is 10, and side AC is 15, which is the hypotenuse side in triangle ABC. Calculate angle x.
An angle x is opposite side AB which is 10, and side AC is 15, which is the hypotenuse side in triangle ABC. Calculate angle x. - Rhomboid
 Calculate the circumference and area of the rhomboid with sides 19 and 20, with their angle 40°.
Calculate the circumference and area of the rhomboid with sides 19 and 20, with their angle 40°. - Sine
 In the triangle Δ ABC, if sin α =0.6 and sin β =0.7 Calculate sin γ.
In the triangle Δ ABC, if sin α =0.6 and sin β =0.7 Calculate sin γ. - Greatest angle
 Calculate the greatest triangle angle with sides 124, 323, 302.
Calculate the greatest triangle angle with sides 124, 323, 302. - Circular sector
 I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector?
I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector? - Hole's angles
 I am trying to find an angle. The top of the hole is .625", and the bottom of the hole is .532". The hole depth is .250". What is the angle of the hole (and what is the formula)?
I am trying to find an angle. The top of the hole is .625", and the bottom of the hole is .532". The hole depth is .250". What is the angle of the hole (and what is the formula)? - Depth angle
 Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115 m above the lake level.
Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115 m above the lake level. - Scalene triangle
 Solve the triangle: A = 50°, b = 13, c = 6
Solve the triangle: A = 50°, b = 13, c = 6
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
