Goniometry and trigonometry - math word problems - page 10 of 32
Number of problems found: 628
- The chimney
 How high is the chimney if we see it from a distance of 60 m at an angle of 42°?
How high is the chimney if we see it from a distance of 60 m at an angle of 42°? - Right triangle
 It is given a right triangle angle alpha of 90 degrees the beta angle of 55 degrees c = 10 cm use the Pythagorean theorem to calculate sides a and b
It is given a right triangle angle alpha of 90 degrees the beta angle of 55 degrees c = 10 cm use the Pythagorean theorem to calculate sides a and b - Triangle α and side
 Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c?
Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c? - Determine 67754
 Adam (A) stands on one river bank, and Bedrich (B) stands on the other. To determine their distance, the base AC with a length of 136 m and the angles CAB with a size of 70°21' and ACB with a size of 43°44' were measured on one river bank. What is the dis
Adam (A) stands on one river bank, and Bedrich (B) stands on the other. To determine their distance, the base AC with a length of 136 m and the angles CAB with a size of 70°21' and ACB with a size of 43°44' were measured on one river bank. What is the dis - Common chord
 The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Two groves
 Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Cross-section - trapezoid
 The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width.
The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width. - Diamond and angles
 The internal angles in the diamond are 60° and 120°. Its side is 5 cm long. Find the area of a diamond.
The internal angles in the diamond are 60° and 120°. Its side is 5 cm long. Find the area of a diamond. - Horizontally 6296
 The camera with a viewing angle of 120 ° was placed horizontally on the observatory at 30 m. What length d of the section at the tower's base can the camera not capture?
The camera with a viewing angle of 120 ° was placed horizontally on the observatory at 30 m. What length d of the section at the tower's base can the camera not capture? - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the - Scalene triangle
 Solve the triangle: A = 50°, b = 13, c = 6
Solve the triangle: A = 50°, b = 13, c = 6 - 30-gon
 The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Determine 83081
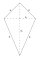 A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid.
A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - Parallelogram
 The sides of the parallelogram are 8 cm and 6 cm long, and the diagonals' angle is 60°. What is its area?
The sides of the parallelogram are 8 cm and 6 cm long, and the diagonals' angle is 60°. What is its area? - Parallelogram - sides L
 In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area.
In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area. - Approaches 45521
 The observer lies on the ground at a distance of 20m from a hunting lodge 5m high. A) At what angle of view does the posed see? B) How much does the angle of view change if it approaches the sitting by 5m?
The observer lies on the ground at a distance of 20m from a hunting lodge 5m high. A) At what angle of view does the posed see? B) How much does the angle of view change if it approaches the sitting by 5m? - Triangle in a square
 In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides.
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Determine 81756
 The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base.
The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base. - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string? - The tower
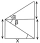 From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
