Grade - math word problems - page 853 of 947
Number of problems found: 18923
- Hexagonal pyramid
 The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high.
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Cube from sphere
 What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm?
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm? - Wood
 Wood density is 0.6 g/cm³. How many kilograms weigh one m³ of wood?
Wood density is 0.6 g/cm³. How many kilograms weigh one m³ of wood? - Chord distance
 The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm.
The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm. - Height of the arc - formula
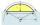 Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this?
Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this? - Wallpaper
 Salesman account for 2.3 meters of wallpaper 149.50 Kc. How much cost 1 meter of wallpaper?
Salesman account for 2.3 meters of wallpaper 149.50 Kc. How much cost 1 meter of wallpaper? - SD - mean
 The mean is 10, and the standard deviation is 3.5. If the data set contains 40 data values, approximately how many of the data values will fall within the range of 6.5 to 13.5?
The mean is 10, and the standard deviation is 3.5. If the data set contains 40 data values, approximately how many of the data values will fall within the range of 6.5 to 13.5? - Angles in triangle
 Calculate the angle alpha in the triangle if the beta is 61 degrees and 98 gamma degrees.
Calculate the angle alpha in the triangle if the beta is 61 degrees and 98 gamma degrees. - Internal and external angles
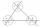 Calculate a triangle's remaining internal and external angles if you know the internal angle γ (gamma) = 34 degrees and one exterior angle is 78 degrees and 40 '. Determine what kind of triangle it is from the size of its angles.
Calculate a triangle's remaining internal and external angles if you know the internal angle γ (gamma) = 34 degrees and one exterior angle is 78 degrees and 40 '. Determine what kind of triangle it is from the size of its angles. - Prism
 The volume of a tetrahedral prism is 2.43 m³. The prism's base is a parallelogram with a side of 2,5dm and height ha = 18cm. Calculate the height of the prism.
The volume of a tetrahedral prism is 2.43 m³. The prism's base is a parallelogram with a side of 2,5dm and height ha = 18cm. Calculate the height of the prism. - Water
 In the garden with an area of 8 ares, rain 40hl of water. To what heights leveled water?
In the garden with an area of 8 ares, rain 40hl of water. To what heights leveled water? - Tetrahedral prism
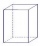 Calculate the surface and volume of a tetrahedral prism, which has a rhomboid-shaped base, and its dimensions are a = 12 cm, b = 7 cm, ha = 6 cm, and prism height h = 10 cm.
Calculate the surface and volume of a tetrahedral prism, which has a rhomboid-shaped base, and its dimensions are a = 12 cm, b = 7 cm, ha = 6 cm, and prism height h = 10 cm. - Circle - easy 2
 The circle has a radius of 6 cm. Calculate its diameter, perimeter, and area:
The circle has a radius of 6 cm. Calculate its diameter, perimeter, and area: - Draw a trapezoid
 Draw a trapezoid if given a = 7 cm, b = 4 cm, c = 3.5 cm, diagonal AC = 5cm. Solve as a construction task.
Draw a trapezoid if given a = 7 cm, b = 4 cm, c = 3.5 cm, diagonal AC = 5cm. Solve as a construction task. - Bicycle wheel
 The bicycle wheel diameter is 62 cm. How many times turns the bicycle on the road 1 km long?
The bicycle wheel diameter is 62 cm. How many times turns the bicycle on the road 1 km long? - Circle - simple
 Calculate the area of a circle in dm² if its circumference is 31.4 cm.
Calculate the area of a circle in dm² if its circumference is 31.4 cm. - Circle from string
 Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle.
Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle. - Clock
 What distance will pass the end of an 8 cm long hour hand for 15 minutes?
What distance will pass the end of an 8 cm long hour hand for 15 minutes? - Colour - billboard
 Shelftalker has the shape of a parallelogram. Its length is 4.9 m, and its corresponding height is 3.5 meters. Calculate how much (kg) paint must be purchased for redecoration if 1 kg covers 4 m² of shelf talker surface.
Shelftalker has the shape of a parallelogram. Its length is 4.9 m, and its corresponding height is 3.5 meters. Calculate how much (kg) paint must be purchased for redecoration if 1 kg covers 4 m² of shelf talker surface. - Office rent
 1 m² of office space is paid €165 per year for rent. How much is the annual rent for an office as big as a football field with dimensions 71.5 m and 102.5 m?
1 m² of office space is paid €165 per year for rent. How much is the annual rent for an office as big as a football field with dimensions 71.5 m and 102.5 m?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
