Examples for secondary school students - page 105 of 231
Number of problems found: 4608
- Two-digit number
 The digit sum of thinking two-digit natural numbers is 11. When it exchanges a sequence of digits, given a number that is 27 less than the thinking number, find out which number I think.
The digit sum of thinking two-digit natural numbers is 11. When it exchanges a sequence of digits, given a number that is 27 less than the thinking number, find out which number I think. - Beads
 How many ways can we thread four red, five blue, and six yellow beads onto a thread?
How many ways can we thread four red, five blue, and six yellow beads onto a thread? - The perimeter of the rectangle
 The length, l, of a rectangle is 4 inches greater than its width, w. The perimeter of the rectangle is at least 30 inches. What inequality shows the range of possible widths of the rectangle?
The length, l, of a rectangle is 4 inches greater than its width, w. The perimeter of the rectangle is at least 30 inches. What inequality shows the range of possible widths of the rectangle? - A loan
 A loan of $944 is charged simple interest at an annual rate of 8.1%. How much money is owed 14 months after the loan was made?
A loan of $944 is charged simple interest at an annual rate of 8.1%. How much money is owed 14 months after the loan was made? - The parabolic segment
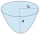 The parabolic segment has a base a = 4 cm and a height v = 6 cm. Calculate the volume of the body that results from the rotation of this segment a) around its base b) around its axis.
The parabolic segment has a base a = 4 cm and a height v = 6 cm. Calculate the volume of the body that results from the rotation of this segment a) around its base b) around its axis. - Together m+w
 Women are 30%. Men are 360 more. How many are together?
Women are 30%. Men are 360 more. How many are together? - Two companies
 The family ordered two companies to modify the garden. The first would be done in 20 days; the second would take 40% less time. How long will they work together if the second company started working when the first worked for four days?
The family ordered two companies to modify the garden. The first would be done in 20 days; the second would take 40% less time. How long will they work together if the second company started working when the first worked for four days? - Stones 3
 Simiyu and Nasike each collected several stones in an arithmetic lesson. If Simiyu gave Nasike 5 stones, Nasike would have twice as many stones as Simiyu. If, initially, Simiyu had five stones less than Nasike, how many stones did each have?
Simiyu and Nasike each collected several stones in an arithmetic lesson. If Simiyu gave Nasike 5 stones, Nasike would have twice as many stones as Simiyu. If, initially, Simiyu had five stones less than Nasike, how many stones did each have? - Bdf tablet
 Detective Harry Thomson has come across a surprising mystery. As part of the weekend's action, the tablet he looked for dropped by 30%. He also recommended this bargain to his friend. However, it came to the shop on Monday, and the tablet was 30% more exp
Detective Harry Thomson has come across a surprising mystery. As part of the weekend's action, the tablet he looked for dropped by 30%. He also recommended this bargain to his friend. However, it came to the shop on Monday, and the tablet was 30% more exp - Washing powder
 A 10-kilogram pack of washing powder is M euros more expensive than a 5-kilogram pack of the same powder. A 5-kilogram package costs P euros. Five kilos of packaging is not worth it because it is more expensive than half the price of 10 kilos. How much is
A 10-kilogram pack of washing powder is M euros more expensive than a 5-kilogram pack of the same powder. A 5-kilogram package costs P euros. Five kilos of packaging is not worth it because it is more expensive than half the price of 10 kilos. How much is - One-time
 A one-time fee of S euros is paid for renting a boat, and the same price is paid for each hour. For H hours of rental, we pay a one-time fee of K euros. Using the variables S, K, and H, determine the time for which we can rent this boat for 20 euros if th
A one-time fee of S euros is paid for renting a boat, and the same price is paid for each hour. For H hours of rental, we pay a one-time fee of K euros. Using the variables S, K, and H, determine the time for which we can rent this boat for 20 euros if th - Cube construction
 A 2×2×2 cube will be constructed using four white and four black unit cube. How many different cubes can be constructed in this way? ( Two cubes are not different if one can be obtained by rotating the other. )
A 2×2×2 cube will be constructed using four white and four black unit cube. How many different cubes can be constructed in this way? ( Two cubes are not different if one can be obtained by rotating the other. ) - Ball bearings
 One bearing is selected from the shipment of ball bearings. It is known from previous deliveries that the inner bearing radius can be considered a normal N distribution (µ = 0.400, σ2 = 25.10^−6). Calculate the probability that the selected radius will ex
One bearing is selected from the shipment of ball bearings. It is known from previous deliveries that the inner bearing radius can be considered a normal N distribution (µ = 0.400, σ2 = 25.10^−6). Calculate the probability that the selected radius will ex - Students
 If the fifth-grade class left 20% of students and in the seventh grade were added two pupils, in the eighth one pupil, the number has not changed in the ninth grade, but it is now tenth students less than it was in the fifth grade. How many pupils are in
If the fifth-grade class left 20% of students and in the seventh grade were added two pupils, in the eighth one pupil, the number has not changed in the ninth grade, but it is now tenth students less than it was in the fifth grade. How many pupils are in - Students 12731
 The 32 quartet students were divided into two classes during the game. After the first round, four students moved from the first class to the second, so half the number of students in the second class were in the first class during the first round. How we
The 32 quartet students were divided into two classes during the game. After the first round, four students moved from the first class to the second, so half the number of students in the second class were in the first class during the first round. How we - Inscribed circle
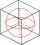 A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - A hammer
 A hammer weighing 500 g hits the nail at a speed of 3 m/s. What is the average force acting on the nail, which penetrates the board to a depth of 5 cm?
A hammer weighing 500 g hits the nail at a speed of 3 m/s. What is the average force acting on the nail, which penetrates the board to a depth of 5 cm? - Energy on impact
 A stone weighing 200 g falls in a free fall for 3 s. Find its kinetic energy on impact.
A stone weighing 200 g falls in a free fall for 3 s. Find its kinetic energy on impact. - Weighing 12471
 Compare the kinetic energy of a man weighing 80 kg who runs at a speed of 2 m/s and missiles weighing 20 g fired at 400 m/s.
Compare the kinetic energy of a man weighing 80 kg who runs at a speed of 2 m/s and missiles weighing 20 g fired at 400 m/s. - Determine 12461
 The 150t aircraft takes off at a speed of 288km/h and, after a while, reaches a speed of 900km/h. Determine the change in the kinetic energy of the aircraft.
The 150t aircraft takes off at a speed of 288km/h and, after a while, reaches a speed of 900km/h. Determine the change in the kinetic energy of the aircraft.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
