Physical quantity - math word problems - page 335 of 346
Number of problems found: 6905
- Trigonometric functions
 In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20)
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - A dodecagon
 Find the surface area of a regular 12-sided polygon if its side is a = 12 cm.
Find the surface area of a regular 12-sided polygon if its side is a = 12 cm. - Inscribed and described circle
 Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm.
Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm. - The cable car
 The cable car is 3,5 kilometers long and climbs at a 30 degrees angle. What is the altitude difference between the Upper and Lower stations?
The cable car is 3,5 kilometers long and climbs at a 30 degrees angle. What is the altitude difference between the Upper and Lower stations? - Bevel
 I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it?
I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it? - Slope of the pool
 Calculate the slope (ratio rise:run) of the bottom of the swimming pool long 40 m. The water depth at the beginning of the pool is 1.09 m (for children), and the depth at the end is 1.88 m (for swimmers). Calculated slope write it as a percentage and also
Calculate the slope (ratio rise:run) of the bottom of the swimming pool long 40 m. The water depth at the beginning of the pool is 1.09 m (for children), and the depth at the end is 1.88 m (for swimmers). Calculated slope write it as a percentage and also - Eiffel Tower
 The Eiffel Tower in Paris is 300 meters high and made of steel. It weighs 8,000 tons. If the tower model made of the same material weighs 2.8 kg, how tall is it?
The Eiffel Tower in Paris is 300 meters high and made of steel. It weighs 8,000 tons. If the tower model made of the same material weighs 2.8 kg, how tall is it? - Triangle sides to angles
 The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle.
The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle. - De Moivre's formula
 There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers.
There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers. - Diagonal
 The diagonal of the rectangle has a length of 39.5 cm. The angle between the diagonal and longer side of the rectangle is 43°. Calculate the area of the rectangle.
The diagonal of the rectangle has a length of 39.5 cm. The angle between the diagonal and longer side of the rectangle is 43°. Calculate the area of the rectangle. - Base and legs
 A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse?
A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse? - Cis notation
 Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation.
Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation. - The staircase
 The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase.
The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase. - One side
 One side is 36 long with a 15° incline. What is the height at the end of that side?
One side is 36 long with a 15° incline. What is the height at the end of that side? - 30-60-90
 The longer leg of a 30°-60°-90° triangle measures 14. What is the length of the shorter leg?
The longer leg of a 30°-60°-90° triangle measures 14. What is the length of the shorter leg? - Doctors
 The drug successfully treats 90% of cases. Calculate the probability that it will cure at least 18 patients out of 20.
The drug successfully treats 90% of cases. Calculate the probability that it will cure at least 18 patients out of 20. - Spacing 82540
 There are 10 trees in a row with the same spacing x = =3 meters. How many meters does a person travel if he waters two trees at once
There are 10 trees in a row with the same spacing x = =3 meters. How many meters does a person travel if he waters two trees at once - SAS calculation
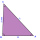 Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal.
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal. - Diagonals in diamond
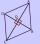 In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals.
In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals. - North Pole
 What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole?
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
