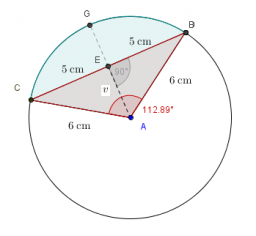
Length of the chord
Calculate the length of the chord in a circle with a radius of 25 cm with a central angle of 26°.
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- inscribed angle theorem
- planimetrics
- Pythagorean theorem
- circle
- triangle
- chord
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Calculate 58953
Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °. - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Magnitude 25411
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Circle sector
The circular sector with a central angle 160° has an area 452 cm². Calculate its radius r.
- Chord MN
Chord MN of the circle has distance from the center circle S 120 cm. Angle MSN is 64°. Determine the radius of the circle. - Subtended 83194
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Circle's 81078
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Arc
What area of a circle occupied the flowers planted in the arc of a circle with a radius 3 m with a central angle of 45°? - Two chords
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords.
- Cone A2V
The cone's surface in the plane is a circular arc with a central angle of 126° and area 415 cm². Calculate the volume of a cone. - Two chords
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords. - Circular sector
I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector? - Cut and cone
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - The central
The central angle of a sector is 30°, and the radius is 15 m. Determine its perimeter.
- Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle. - Central angle
The circle has a diameter of 46 cm. What is the arc length corresponds to a central angle of 30°? - Circular 21273 The dragon has the shape of a circular section with a central angle of 40 ° and a radius of 35 cm. How much paper do we need to make if 10% is added to the curved ones?
