Maths practice for 14 year olds - page 193 of 370
Number of problems found: 7395
- Three-digit 9531
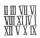 How many three-digit numbers do not change if we replace the digit in the hundreds with the digit in the units?
How many three-digit numbers do not change if we replace the digit in the hundreds with the digit in the units? - Bodybuilder 9521
 The bodybuilder weighs 96 kg. The second bodybuilder weighs 25% more than the first bodybuilder. What is the sum of their weights?
The bodybuilder weighs 96 kg. The second bodybuilder weighs 25% more than the first bodybuilder. What is the sum of their weights? - Grandmother 9451
 Petr and Honza received 315 CZK from their grandmother. Petr Dostál a third more than Honza. How many crowns did each of them have?
Petr and Honza received 315 CZK from their grandmother. Petr Dostál a third more than Honza. How many crowns did each of them have? - Tax and death
 Calculate 60% (aggregate taxes and levies) of 1000 euros of the gross wage.
Calculate 60% (aggregate taxes and levies) of 1000 euros of the gross wage. - Rectangular 9401
 Matrix E is a rectangular matrix that contains 48 elements and four rows. How many columns does this matrix have?
Matrix E is a rectangular matrix that contains 48 elements and four rows. How many columns does this matrix have? - Dimensions 9371
 Change both dimensions of the rectangle in a ratio of 5:3. Initially, the dimensions are 9cm and 15cm. What are the dimensions of the rectangle after the change?
Change both dimensions of the rectangle in a ratio of 5:3. Initially, the dimensions are 9cm and 15cm. What are the dimensions of the rectangle after the change? - Tree trunk
 What is the smallest diameter of a tree trunk that we can cut a square-section square with a side length of 20 cm?
What is the smallest diameter of a tree trunk that we can cut a square-section square with a side length of 20 cm? - Divisible 9331
 The number X is the smallest natural number whose half is divisible by three, a third is divisible by four, a quarter is divisible by eleven, and its half gives a remainder of 5 when divided by seven. Find this number.
The number X is the smallest natural number whose half is divisible by three, a third is divisible by four, a quarter is divisible by eleven, and its half gives a remainder of 5 when divided by seven. Find this number. - Significant 9321
 Only herbs with 5 and 7 leaves grow in the Old Forest. When the boar Vavřínec collects raw materials for herbal liquor, it always tears off the whole herb and puts it in a basket. What is the most significant number of letters he will ever manage to have
Only herbs with 5 and 7 leaves grow in the Old Forest. When the boar Vavřínec collects raw materials for herbal liquor, it always tears off the whole herb and puts it in a basket. What is the most significant number of letters he will ever manage to have - Geometric progressiob
 If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms.
If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms. - Calculate 9221
 There are two sloths in the tree's branches. One is 2.5 m from the trunk, and the other is on the other side of the tree, 4 m from the trunk. The sloths head out to get to know each other. Calculate how far from the log they will meet if they climb at the
There are two sloths in the tree's branches. One is 2.5 m from the trunk, and the other is on the other side of the tree, 4 m from the trunk. The sloths head out to get to know each other. Calculate how far from the log they will meet if they climb at the - Circumference 9211
 The rectangle has a circumference of 30 cm, and its width is 3 cm shorter than its length. What is its area?
The rectangle has a circumference of 30 cm, and its width is 3 cm shorter than its length. What is its area? - Two places
 The distance to the places is 60 km. From A place, a pedestrian came out at a speed of 4 km/h, and at the same time, a car drove against him from place B. What was the car's speed if the pedestrian met him in 90 minutes?
The distance to the places is 60 km. From A place, a pedestrian came out at a speed of 4 km/h, and at the same time, a car drove against him from place B. What was the car's speed if the pedestrian met him in 90 minutes? - Procedure 9191
 Behind the tractor, which travels at 12 km/h, they sent a car 3.5 hours later to catch up with him in 45 minutes. What speed does he have to go? Please also explain the procedure.
Behind the tractor, which travels at 12 km/h, they sent a car 3.5 hours later to catch up with him in 45 minutes. What speed does he have to go? Please also explain the procedure. - Two friends
 Two friends on a bicycle rode against each other from two places 49 km apart. The first set off at 8.00 at a speed of 20km/h, the second 12 minutes later at a speed of 25km/h. What time do they meet? How many km will each of them travel since then?
Two friends on a bicycle rode against each other from two places 49 km apart. The first set off at 8.00 at a speed of 20km/h, the second 12 minutes later at a speed of 25km/h. What time do they meet? How many km will each of them travel since then? - Achilles and the turtle
 It is known that Achilles will not catch up with the turtle. But his brother Auchalles can do it. He even gave the turtle an 8-hour lead. Calculate how far from the start Auchalles will meet a turtle moving at an average speed of 70 m/h if Auchalles walks
It is known that Achilles will not catch up with the turtle. But his brother Auchalles can do it. He even gave the turtle an 8-hour lead. Calculate how far from the start Auchalles will meet a turtle moving at an average speed of 70 m/h if Auchalles walks - Checkerboard 9091
 Determine how many ways we can place 5 different pieces on an 8x8 chessboard so that two are on black squares and three are on white squares.
Determine how many ways we can place 5 different pieces on an 8x8 chessboard so that two are on black squares and three are on white squares. - Balls
 From the bag with numbered balls (numbers 1,2,3,. ..20), we pick one ball. What is the probability of choosing a number containing 1?
From the bag with numbered balls (numbers 1,2,3,. ..20), we pick one ball. What is the probability of choosing a number containing 1? - Base of prism
 The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm².
The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm². - Time passing
 Six years ago, Marcela's mother was two times older than her and two times younger than her father. When Marcela is 36, she will be twice as young as her father. How old are Marcela, her father, and her mother now?
Six years ago, Marcela's mother was two times older than her and two times younger than her father. When Marcela is 36, she will be twice as young as her father. How old are Marcela, her father, and her mother now?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
