Rectangle practice problems - page 46 of 49
Number of problems found: 969
- Octagon from rectangle
We cut the corners of a rectangular tablecloth with dimensions of 4 dm and 8 dm into isosceles triangles. Thus, the octagon formed had an area of 26 dm². How many dm² of tablecloth do we cut down? - Axial section
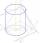The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder. - Black building
Jozef built building with a rectangular shape 3.9 m × 6.7 m. Calculate how much percent exceeded the limit 25 m² for a small building. A building not built by the law is called a "black building". Calculate the angle that the walls were clenching each oth - Again saw
We have a sculpture beam from the tree trunk with a rectangular cross-section with dimensions 91 mm and 87 mm. What is the trunk's smallest diameter? - Rectangular base pyramid
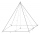The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid. - Quadrangle ACEG
The figure shows two rectangles ABCD and DEFG, with |DE|=3 CM, |AD|=6 CM, |DG|= 5, |CD|= 10 CM. Calculate the area of quadrangle ACEG. Figure description: the rectangles have one vertex D in common. Rectangle ABCD has twice as long sides as DEFG. All si - Rectangle
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - Horizontally 8187
We turn the prism-shaped box with a height of 1 m and a square base with an edge of 0.6 m under a force of 350 N, which acts horizontally compared to the upper edge. What is the weight of the box? - Circumscribed 2671
The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle. - Faces diagonals
Find the cuboid volume if the cuboid's diagonals are x, y, and z (wall diagonals or three faces). Solve for x=1.6, y=1.8, z=1.6 - Quadrilateral pyramid Calculate the volume of a quadrilateral pyramid, the base of which has the shape of a rectangle with dimensions a = 6cm, b = 4cm, and height v = 11cm
- Wall and body diagonals
Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m - Quadrilateral pyramid
Construct a 3D model of a quadrilateral pyramid with a rectangle base and sides of isosceles triangles, with a volume of 80 cubic cm. I need to know the sides and the height. - Diameter 6032
The road roller is 2 m long and 1 m in diameter. How many square meters of road roll when it turns 15 times? - Rectangle
In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle? - Ladder
A 4 m long ladder touches the cube 1mx1m at the wall. How high reach on the wall? - Corresponding 6021
How much paint do we need to paint a pool in the shape of a 6-sided prism? The base edge measures 21 dm, the corresponding height is 1.8 m, and the pool height is 150 cm. We need 0.21 kg of paint per 1 m². - Tetrahedral pyramid 8
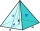Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=40° B=70° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - Prism - box
The prism's base is a rectangle with a side of 7.5 cm and 12.5 cm diagonal. The volume of the prism is V = 0.9 dm³. Calculate the surface of the prism. - Maximum area of rhombus
Calculate the interior angles at which the equilateral rhombus has a maximum area.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
