Solid geometry, stereometry - page 2 of 121
Number of problems found: 2409
- Three cubes
 Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube.
Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube. - Spheres to cone
 Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed. - Melting 3 cubes
 The sides of the three metal cubes are 30 cm, 40 cm, and 50 cm, respectively. Find the side of the new cube formed by melting these cubes together.
The sides of the three metal cubes are 30 cm, 40 cm, and 50 cm, respectively. Find the side of the new cube formed by melting these cubes together. - A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - Jane and tent
 Jane and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then,
Jane and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then, - Geometric Solid
 A concrete pipe is 1.0 m long. The inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (in cubic meters) needed to make 25 pieces of pipe?
A concrete pipe is 1.0 m long. The inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (in cubic meters) needed to make 25 pieces of pipe? - Saria
 Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box?
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - Lamp shade
 A lamp shade is in the form of a frustum of a cone with slant height 7 in., radii of bases 3 in. and 7 in. respectively. How much material is used in its construction if ¼ in. is allowed for the seam.
A lamp shade is in the form of a frustum of a cone with slant height 7 in., radii of bases 3 in. and 7 in. respectively. How much material is used in its construction if ¼ in. is allowed for the seam. - Eva wraps
 Eva wraps a gift box in the shape of a right rectangular prism. The figure shows a net for the gift box. How much wrapping paper did she use, in square meters?
Eva wraps a gift box in the shape of a right rectangular prism. The figure shows a net for the gift box. How much wrapping paper did she use, in square meters? - A capsule
 A medicine capsule is a cylinder with two hemispheres stuck to each end. Its length is 14 mm, and its diameter is 5 mm. Find its surface area.
A medicine capsule is a cylinder with two hemispheres stuck to each end. Its length is 14 mm, and its diameter is 5 mm. Find its surface area. - The area 4
 In square decimeters, how much is the area of a cylinder with a height of 2 dm and a diameter of 1 dm? "
In square decimeters, how much is the area of a cylinder with a height of 2 dm and a diameter of 1 dm? " - Prism - base and height
 Find volume of the prism if the base area equals 20 inches² with the height is 12 inches.
Find volume of the prism if the base area equals 20 inches² with the height is 12 inches. - New drink
 Create a new drink can that will double the volume of the original can used. The dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : O
Create a new drink can that will double the volume of the original can used. The dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : O - Spire - prism
 Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m. - A piece 7
 A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice.
A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice. - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - A triangular prism
 Find the number of faces, edges, and vertices of a triangular prism.
Find the number of faces, edges, and vertices of a triangular prism. - The cup
 In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure.
In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure. - Storage shed
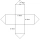 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
