Solid geometry, stereometry - page 34 of 121
Number of problems found: 2418
- The surface
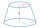The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Cube surfce2volume
Calculate the volume of the cube if its surface is 150 cm². - Spherical segment
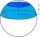Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm. - The cube The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume.
- Diameter = height
The cylinder's surface, the height of which is equal to the diameter of the base, is 4239 cm square. Calculate the cylinder volume. - Truncated cone and sphere
A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter? - Cube edge
The cube has a surface area of 110.6 cm². Calculate the length of its edge. - Length = 3 width
The length of a cuboid is thrice its width. The height and volume of the cuboid measure 4cm and 300 cubic cm, respectively. What is the length of this cuboid? - Cube weight comparison
The cube weighs 32 kg. How much kg does a cube made of the same material, which has an edge four times shorter, weigh? - Length of the edge
Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number. - Cylinder surface calculation
The area of the cylinder shell is 300 cm², the height of which is equal to the diameter of the base. Find the surface of the cylinder. - Sphere radius calculation
Calculate the radius of a sphere with a volume of 6.2 dm3, round to the nearest centimeter. - Cube surface and volume
The surface of the cube is 500 cm². How much cm³ will its volume be? - Aquarium 20
Martin wanted to help his father glue together an aquarium. He read in the manual that it should have a volume of 45 liters. But he didn't have much space on the table, the bottom of the aquarium could only be 25 cm and 40 cm. How high does the aquarium h - Cylinder diameter height
The cylinder's volume is 5l, and its height is equal to half the diameter of the base. Find the dimensions of the cylinder. - Dice edge size
The dice have a volume of 80 cm³. Calculate the edge size in mm. - Edges or sides
Calculate the cube volume if the sum of the lengths of all sides is 276 cm. - Tank diameter
A cylindrical tank has a volume of 60 hectoliters and is 2.5 meters deep. Calculate the tank diameter. - The cube
The cube has a surface of 600 cm². What is its volume? - Water ball diameter
The water ball has a volume of 32,500 m³. How big is its diameter?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
