Sphere practice problems - page 11 of 12
Number of problems found: 231
- The cylindrical container
 The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting, how many balls does water flow over the edge of the con
The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting, how many balls does water flow over the edge of the con - Gold ring
 A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i
A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i - Portioning ice cream
 How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure.
How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure. - Sphere cut
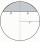 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Spherical 63214
 The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca
The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca - Spherical cap
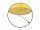 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - Circumference 81557
 Calculate how many volleyballs with a circumference of 65 cm fit into a cube-shaped rack whose edge is 100 cm long.
Calculate how many volleyballs with a circumference of 65 cm fit into a cube-shaped rack whose edge is 100 cm long. - Spherical segment
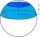 Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm.
Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm. - Truncated cone and sphere
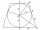 A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter?
A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter? - Spherical 81527
 Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume?
Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume? - Spherical segment
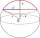 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Alien ship
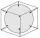 The alien ship has the shape of a sphere with a radius of r = 3000m, and its crew needs the ship to carry the collected research material in a cuboid box with a square base. Determine the length of the base and (and height h) so that the box has the large
The alien ship has the shape of a sphere with a radius of r = 3000m, and its crew needs the ship to carry the collected research material in a cuboid box with a square base. Determine the length of the base and (and height h) so that the box has the large - Inscribed circle
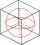 A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - Sphere parts, segment
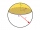 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment? - Stadium
 A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter.
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - Sphere submerged in the cone
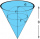 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Larger sphere
 The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³.
The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³. - Spherical cap
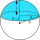 Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap).
Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap). - Spherical sector
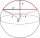 Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm.
Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm. - Hemisphere - roof
 The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint
The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
