Square root - math word problems - page 16 of 69
Number of problems found: 1376
- Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Playground 79454
 In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t
In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t - Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - General triangle
 Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle.
Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle. - Calculate the chord
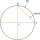 The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle.
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - The circle
 If the radius of a circle is 3+root3, what is the area?
If the radius of a circle is 3+root3, what is the area? - Quadrilateral 78874
 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Calculate 78714
 Calculate the size of the base and side of an isosceles triangle if the side is 1 cm longer than the base and the height to the base is 2 cm shorter than the side.
Calculate the size of the base and side of an isosceles triangle if the side is 1 cm longer than the base and the height to the base is 2 cm shorter than the side. - The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - Hydraulic jack
 Hydraulic jack has a capacity of 10 tons. The hydraulic lifter has 6 cm² and 360 cm² pistons. Determine the diameter of the small piston (d) and the force I will create on the piston (F). Design a single-reverse and a double-reverse lever.
Hydraulic jack has a capacity of 10 tons. The hydraulic lifter has 6 cm² and 360 cm² pistons. Determine the diameter of the small piston (d) and the force I will create on the piston (F). Design a single-reverse and a double-reverse lever. - Swimming 78124
 A 16 m square swimming pool has an area of 1 m² on the city plan. What is the scale of the city plan?
A 16 m square swimming pool has an area of 1 m² on the city plan. What is the scale of the city plan? - The rectangle 5
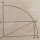 The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - The triangle 5
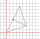 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Cuboid's diagonal
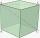 The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid?
The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid? - RT a-b-x
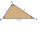 There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd.
There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd. - Dipole - complex power
 For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice.
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice. - A cube
 A cube has a surface area of 64 ft². Henrietta creates a reduction of this cube using a scale factor of 0.5. What is the surface area of the reduction?
A cube has a surface area of 64 ft². Henrietta creates a reduction of this cube using a scale factor of 0.5. What is the surface area of the reduction? - Polygon 3
 Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation?
Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation? - Isosceles triangle
 Find the area of an isosceles triangle whose leg is twice the base, b=1
Find the area of an isosceles triangle whose leg is twice the base, b=1 - Evaluate 26
 Evaluate square root: √1³+2³+3³+4³=
Evaluate square root: √1³+2³+3³+4³=
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
