Square root - math word problems - page 59 of 69
Number of problems found: 1376
- Calculation
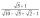 How much is the sum of the square root of six and the square root of 100?
How much is the sum of the square root of six and the square root of 100? - Square roots
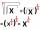 What is equal to the product of the square roots of 410881?
What is equal to the product of the square roots of 410881? - ISO Triangle V2
 The perimeter of the isosceles triangle is 474 m, and the base is 48 m longer than the arms. Calculate the area of this triangle.
The perimeter of the isosceles triangle is 474 m, and the base is 48 m longer than the arms. Calculate the area of this triangle. - Triangular prism
 The base perpendicular triangular prism is a right triangle whose hypotenuse measures 14 cm and one cathetus 9 cm. The height of the prism is equal to 2/9 of the base's perimeter. Calculate the surface area of the prism.
The base perpendicular triangular prism is a right triangle whose hypotenuse measures 14 cm and one cathetus 9 cm. The height of the prism is equal to 2/9 of the base's perimeter. Calculate the surface area of the prism. - ISO trapezoid v2
 The bases of the isosceles trapezoid are measured 20 cm and 4 cm, and their perimeter is 55 cm. What is the area of a trapezoid?
The bases of the isosceles trapezoid are measured 20 cm and 4 cm, and their perimeter is 55 cm. What is the area of a trapezoid? - Pit
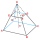 The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n
The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n - Triangular prism
 The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism.
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - Mystery of stereometry
 Two regular tetrahedrons have surfaces 92 cm² and 207 cm². In what ratio are their volumes? Write as a fraction and as a decimal rounded to 4 decimal places.
Two regular tetrahedrons have surfaces 92 cm² and 207 cm². In what ratio are their volumes? Write as a fraction and as a decimal rounded to 4 decimal places. - Catheti
 The hypotenuse of a right triangle is 35, and the sum of legs is 49. Calculate the length of its legs.
The hypotenuse of a right triangle is 35, and the sum of legs is 49. Calculate the length of its legs. - Cone and the ratio
 The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface.
The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface. - Sails
 We know the heights of sail, 220, 165, and 132. It has a triangular shape. What is the surface of the sail?
We know the heights of sail, 220, 165, and 132. It has a triangular shape. What is the surface of the sail? - Suzan
 My daughter reaches X years in X squared, said Susan's father in 1996 during her birthday celebration. When will the given fact become a reality, and how many years at that time will Susan have?
My daughter reaches X years in X squared, said Susan's father in 1996 during her birthday celebration. When will the given fact become a reality, and how many years at that time will Susan have? - De Moivre's formula
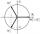 There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers.
There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers. - Tiles
 From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles.
From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles. - Ladder
 10 meters long ladder is leaning against the wall of the well, and its lower end is 1 meters from this wall. How high from the bottom of a well is the top edge of the ladder?
10 meters long ladder is leaning against the wall of the well, and its lower end is 1 meters from this wall. How high from the bottom of a well is the top edge of the ladder? - Triangle
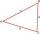 The triangle has known all three sides: a=4.6 m, b=7.4 m, c= 3.8 m. Calculate the area of this triangle.
The triangle has known all three sides: a=4.6 m, b=7.4 m, c= 3.8 m. Calculate the area of this triangle. - Box
 The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a
The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a - Diamond
 The rhombus has a side 22 cm and one diagonal 35 cm long. Calculate its area.
The rhombus has a side 22 cm and one diagonal 35 cm long. Calculate its area. - Roots
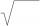 Calculate the square root of these numbers:
Calculate the square root of these numbers: - Distance
 What is the distance between the origin and the point (-11; 13)?
What is the distance between the origin and the point (-11; 13)?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
