Square root - math word problems - page 60 of 69
Number of problems found: 1376
- Vector sum
 The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v?
The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v? - Pizza
 Pizza with a diameter of 40 cm weights 409 g. What diameter will a pizza weigh 764 g made from the same cloth (same thickness) and decorated?
Pizza with a diameter of 40 cm weights 409 g. What diameter will a pizza weigh 764 g made from the same cloth (same thickness) and decorated? - Diagonals
 Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - Inscribed rectangle
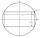 The circle area is 231. Determine the area of the inscribed rectangle with one side 13 long.
The circle area is 231. Determine the area of the inscribed rectangle with one side 13 long. - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21)
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - Diameter
 If the endpoints of the diameter of a circle are A(10, -10) and B (9, -2), what is the circle's radius?
If the endpoints of the diameter of a circle are A(10, -10) and B (9, -2), what is the circle's radius? - Chord - TS v2
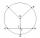 The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS?
The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS? - Isosceles IV
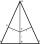 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Funnel
 The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 8.1 liters of water.
The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 8.1 liters of water. - Round table
 A round table with a diameter d = 133 cm is coated by a square tablecloth with a side length 156 cm. About how many cm is the higher center of the tablecloth than its corners?
A round table with a diameter d = 133 cm is coated by a square tablecloth with a side length 156 cm. About how many cm is the higher center of the tablecloth than its corners? - Prism X
 The prism with the edges of the lengths x cm, 2x cm, and 3x cm has a volume 29478 cm³. What is the area of the surface of the prism?
The prism with the edges of the lengths x cm, 2x cm, and 3x cm has a volume 29478 cm³. What is the area of the surface of the prism? - Tower
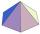 The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste.
The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste. - Axial section
 The axial section of the cylinder is diagonal 45 cm long, and we know that the area of the side and the base area are in ratio 6:5. Calculate the height and radius of the cylinder base.
The axial section of the cylinder is diagonal 45 cm long, and we know that the area of the side and the base area are in ratio 6:5. Calculate the height and radius of the cylinder base. - Equation
 Equation -3x²+bx -108 =0 has one root x1 = 1. Determine the coefficient b and the second root x2.
Equation -3x²+bx -108 =0 has one root x1 = 1. Determine the coefficient b and the second root x2. - RT 10
 The area of the right triangle is 15 cm², and one of its catheti is a=7 cm. Calculate the perimeter of the triangle ABC.
The area of the right triangle is 15 cm², and one of its catheti is a=7 cm. Calculate the perimeter of the triangle ABC. - Bomber
 The aircraft flies at an altitude of 14700 m above the ground at a speed of 619 km/h. At what horizontal distance from point B should be released any body from the aircraft body fall into point B? (g = 9.81 m/s²)
The aircraft flies at an altitude of 14700 m above the ground at a speed of 619 km/h. At what horizontal distance from point B should be released any body from the aircraft body fall into point B? (g = 9.81 m/s²) - OPT
 What is the perimeter of a right triangle with the legs 11 cm and 24 cm long?
What is the perimeter of a right triangle with the legs 11 cm and 24 cm long? - Elevation
 What must be an observer's elevation so that he may see an object on the Earth 866 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
What must be an observer's elevation so that he may see an object on the Earth 866 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km. - Horizon
 The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.]
The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Square side
 Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0.
Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
