Square (second power, quadratic) - math word problems - page 74 of 150
Number of problems found: 2994
- Quadrilateral pyramid
 The regular quadrilateral pyramid has a base circumference of 44 cm and a body height of 3.2 cm. Calculate its volume and surface.
The regular quadrilateral pyramid has a base circumference of 44 cm and a body height of 3.2 cm. Calculate its volume and surface. - Paper cut
 How many 9 cm² figures can we cut from 36 dm² paper?
How many 9 cm² figures can we cut from 36 dm² paper? - Cross five
 The figure in the picture is composed of the same squares and has an area of 45cm². What is its perimeter?
The figure in the picture is composed of the same squares and has an area of 45cm². What is its perimeter? - Calculate 14733
 Square has the side a = 12 cm. Calculate the area of a triangle in the square.
Square has the side a = 12 cm. Calculate the area of a triangle in the square. - One third power
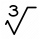 Which equation justifies why ten to the one-third power equals the cube root of ten?
Which equation justifies why ten to the one-third power equals the cube root of ten? - Two 2D shapes
 Decide which shapes have more area: (a) a square of 8cm side, or (b) two rectangles with sides of 5cm and 15cm? Write the result as 1 or 2 (rectangles)
Decide which shapes have more area: (a) a square of 8cm side, or (b) two rectangles with sides of 5cm and 15cm? Write the result as 1 or 2 (rectangles) - Axial section of the cone
 The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square.
The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square. - Length of the edge
 Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number.
Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number. - Unpainted 14513
 The abcd square is composed of 36 small squares. Six of them are painted. How many small squares do we still need to color so that a quarter of the area of the abcd square remains unpainted?
The abcd square is composed of 36 small squares. Six of them are painted. How many small squares do we still need to color so that a quarter of the area of the abcd square remains unpainted? - Increases 14471
 How many percent will it increase a) surface b) cube volume if the edge of the cube increases by 25%?
How many percent will it increase a) surface b) cube volume if the edge of the cube increases by 25%? - Plot
 The land is in the shape of a square with a dimension of 22 meters. How much will we pay for the fence around the entire plot?
The land is in the shape of a square with a dimension of 22 meters. How much will we pay for the fence around the entire plot? - Moreover 14393
 The land is in the shape of a square with a side of 65.4 meters. Moreover, 1 meter of mesh costs 2.30 euros. How many euros do we pay for fencing land?
The land is in the shape of a square with a side of 65.4 meters. Moreover, 1 meter of mesh costs 2.30 euros. How many euros do we pay for fencing land? - Dimensions 14383
 The living room has dimensions of 40 dm and 50 dm. A square meter of wooden floor costs 13 euros. How much do we pay to lay a wooden floor in the living room?
The living room has dimensions of 40 dm and 50 dm. A square meter of wooden floor costs 13 euros. How much do we pay to lay a wooden floor in the living room? - Measuring 14343
 The town square has the shape of a square measuring 510 meters. What is the size of this square?
The town square has the shape of a square measuring 510 meters. What is the size of this square? - Rectangular 14333
 The rectangular plot has an area of 200 square meters. The length of the land is 20 meters. How wide is the land?
The rectangular plot has an area of 200 square meters. The length of the land is 20 meters. How wide is the land? - Square-shaped 14271
 We should sow grass in a square-shaped garden with a side of 16.2 m. How many kg of grass seed do we need? One square meter is necessary for 25 grams.
We should sow grass in a square-shaped garden with a side of 16.2 m. How many kg of grass seed do we need? One square meter is necessary for 25 grams. - Perimeter of the circle
 Calculate the perimeter of the circle in dm, whose radius equals the side of the square containing 0.49 dm².
Calculate the perimeter of the circle in dm, whose radius equals the side of the square containing 0.49 dm². - Pool
 How many hectoliters of water is in a cuboid pool (a = 25m, b = 8m) if the area of the wetted walls is 279.2 m²?
How many hectoliters of water is in a cuboid pool (a = 25m, b = 8m) if the area of the wetted walls is 279.2 m²? - Quadrilateral prism + water
 We poured water up to a height of 34 cm into a container of a regular quadrilateral prism with a base edge a = 10.6 cm and a wall diagonal of 3.9 dm. We then inserted a 6 cm long cylinder with a diameter of 10 cm. How many liters of water overflowed?
We poured water up to a height of 34 cm into a container of a regular quadrilateral prism with a base edge a = 10.6 cm and a wall diagonal of 3.9 dm. We then inserted a 6 cm long cylinder with a diameter of 10 cm. How many liters of water overflowed? - A square base
 A solid right pyramid has a square base. The base edge length is 4 centimeters, and the pyramid's height is 3 centimeters. What is the volume of the pyramid?
A solid right pyramid has a square base. The base edge length is 4 centimeters, and the pyramid's height is 3 centimeters. What is the volume of the pyramid?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
