A rectangle 2
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Check out our ratio calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- The diamond
The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond. - Calculate 70814
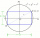The lengths of the sides AB and AD of the rectangle ABCD are in the ratio 3:4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - The sides
The sides of a rectangle are in a ratio of 2:3, and its perimeter is 1 1/4 inches. What are the lengths of its side? Draw it. - The sides
The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals - RT with rectangle
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - The perimeter
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - Perimeter - rectangle
The perimeter of the rectangle is about cm. One side is three times smaller than the other. Express the lengths of both sides of the rectangle using its perimeter
