The trapezium
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
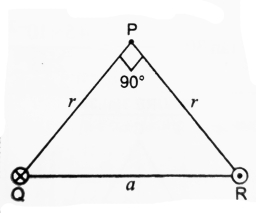
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Isosceles weight
 A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight?
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight? - Right-angled 4951
 Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5
Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5 - Isosceles trapezium
 Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm.
Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm. - ISO trapezium
 Calculate the area of an isosceles trapezoid with base 50 long, leg 12 long, and with the angle between the base and leg 70 degrees.
Calculate the area of an isosceles trapezoid with base 50 long, leg 12 long, and with the angle between the base and leg 70 degrees. - Right-angled triangle base
 Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of the prism is 24 cm.
Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of the prism is 24 cm. - Isosceles triangle
 Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm.
Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm. - Slant height 3
 The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height.
The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height.
