Themes, topics - math word problems - page 98 of 168
Number of problems found: 3360
- The glass
 1 m³ of glass weighs 2600 kg. Calculate the weight of the glass glazing panel with dimensions of 2.5 m and 3.8 m if the thickness of the glass is 0.8 cm.
1 m³ of glass weighs 2600 kg. Calculate the weight of the glass glazing panel with dimensions of 2.5 m and 3.8 m if the thickness of the glass is 0.8 cm. - Play tennis
 Peter and Jirka agreed to go play tennis. Peter's path to the tennis court is 800 meters longer and leads around Jirka's house. Peter comes out first and then picks up Jirka. Together they go at the same average speed as Peter went, so they reach the plac
Peter and Jirka agreed to go play tennis. Peter's path to the tennis court is 800 meters longer and leads around Jirka's house. Peter comes out first and then picks up Jirka. Together they go at the same average speed as Peter went, so they reach the plac - Sloth meeting distance
 There are two sloths in the tree's branches. One is 2.5 m from the trunk, and the other is on the other side of the tree, 4 m from the trunk. The sloths head out to get to know each other. Calculate how far from the log they will meet if they climb at the
There are two sloths in the tree's branches. One is 2.5 m from the trunk, and the other is on the other side of the tree, 4 m from the trunk. The sloths head out to get to know each other. Calculate how far from the log they will meet if they climb at the - Two places
 The distance to the places is 60 km. From A place, a pedestrian came out at a speed of 4 km/h, and at the same time, a car drove against him from place B. What was the car's speed if the pedestrian met him in 90 minutes?
The distance to the places is 60 km. From A place, a pedestrian came out at a speed of 4 km/h, and at the same time, a car drove against him from place B. What was the car's speed if the pedestrian met him in 90 minutes? - Car tractor pursuit
 Behind the tractor, which travels at 12 km/h, they sent a car 3.5 hours later to catch up with him in 45 minutes. What speed does he have to go? Please also explain the procedure.
Behind the tractor, which travels at 12 km/h, they sent a car 3.5 hours later to catch up with him in 45 minutes. What speed does he have to go? Please also explain the procedure. - Two friends
 Two friends on a bicycle rode against each other from two places 49 km apart. The first set off at 8.00 at a speed of 20km/h, the second 12 minutes later at a speed of 25km/h. What time do they meet? How many km will each of them travel since then?
Two friends on a bicycle rode against each other from two places 49 km apart. The first set off at 8.00 at a speed of 20km/h, the second 12 minutes later at a speed of 25km/h. What time do they meet? How many km will each of them travel since then? - Achilles and the turtle
 It is known that Achilles will not catch up with the turtle. But his brother Auchalles can do it. He even gave the turtle an 8-hour lead. Calculate how far from the start Auchalles will meet a turtle moving at an average speed of 70 m/h if Auchalles walks
It is known that Achilles will not catch up with the turtle. But his brother Auchalles can do it. He even gave the turtle an 8-hour lead. Calculate how far from the start Auchalles will meet a turtle moving at an average speed of 70 m/h if Auchalles walks - RPM
 An electric motor makes 3,000 revolutions per minute. How many degrees does it rotate in one second?
An electric motor makes 3,000 revolutions per minute. How many degrees does it rotate in one second? - The hiker
 The hiker will travel 40% of the route on the first day and 1/3 of the rest on the second day. Last day 30 km. What was the length of the 3-day trip? How many kilometers did he walk each day?
The hiker will travel 40% of the route on the first day and 1/3 of the rest on the second day. Last day 30 km. What was the length of the 3-day trip? How many kilometers did he walk each day? - Reserve map scale
 The nature reserve covers an area of 40,000 square kilometers. If we draw it on a map on a scale of 1:1000000, we get a square. Find the side of the square on the map.
The nature reserve covers an area of 40,000 square kilometers. If we draw it on a map on a scale of 1:1000000, we get a square. Find the side of the square on the map. - Average speed
 The truck drove 1/2 of the way on the highway at 80 km/h. The other half of the way, 20 km/h. Calculate the average speed.
The truck drove 1/2 of the way on the highway at 80 km/h. The other half of the way, 20 km/h. Calculate the average speed. - Two parts journey
 The driver of the car plans to drive 30 km in 0.5 hours. For 20 minutes he follows the convoy (traffic jam) at a speed of 30 km/h. What speed would he have to go in the remaining time?
The driver of the car plans to drive 30 km in 0.5 hours. For 20 minutes he follows the convoy (traffic jam) at a speed of 30 km/h. What speed would he have to go in the remaining time? - Three pumps together
 One pump fills the tank in 1.5 hours, the second in 2 hours, and the third in 3 hours 20 minutes. How many minutes will the tank fill with three pumps if they work simultaneously?
One pump fills the tank in 1.5 hours, the second in 2 hours, and the third in 3 hours 20 minutes. How many minutes will the tank fill with three pumps if they work simultaneously? - Bicycle pursuit calculation
 The first patrol of the pupils' orientation run started at 8 a.m. at an average speed of 5 km/h. At 8:36 AM, the leader of the orienteering race followed them on a bicycle at a speed of 20 km/h. When and how far from the start will he catch up with them?
The first patrol of the pupils' orientation run started at 8 a.m. at an average speed of 5 km/h. At 8:36 AM, the leader of the orienteering race followed them on a bicycle at a speed of 20 km/h. When and how far from the start will he catch up with them? - Copper sulphate
 How much g of water do we have to add to 240 g of an 84% CuSO4 solution to produce a 60% solution? (Express the mass of crystalline CuSO4 in the original solution and the resulting solution and compare them. )
How much g of water do we have to add to 240 g of an 84% CuSO4 solution to produce a 60% solution? (Express the mass of crystalline CuSO4 in the original solution and the resulting solution and compare them. ) - Triangle area ratio
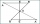 In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P
In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Records
 Records indicate 90% error-free. If eight records are randomly selected, what is the probability that at least two records have no errors?
Records indicate 90% error-free. If eight records are randomly selected, what is the probability that at least two records have no errors? - Car distance calculation
 The car's speedometer showed a constant speed of 60 km/h for 5 minutes. What path did the car cover during this time?
The car's speedometer showed a constant speed of 60 km/h for 5 minutes. What path did the car cover during this time? - Density - Au
 What volume is 1/2 kg of gold? The density of gold is 19.3 kg/dm³.
What volume is 1/2 kg of gold? The density of gold is 19.3 kg/dm³. - Motorcyclist average speed
 The motorcyclist was riding: a) the first half of the driving time at a speed of 30 km/h, the second half of the time at a speed of 60 km/h, b) the track's first half at a speed of 30 km/h and the second half at a speed of 60 km/h. Determine its average s
The motorcyclist was riding: a) the first half of the driving time at a speed of 30 km/h, the second half of the time at a speed of 60 km/h, b) the track's first half at a speed of 30 km/h and the second half at a speed of 60 km/h. Determine its average s
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
