Trapezoid practice problems - page 7 of 15
Number of problems found: 288
- Trapezium ABCD
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Circumference 7052
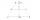The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Embankment
The perpendicular cross-section of the embankment around the lake has the shape of an isosceles trapezoid. Calculate the perpendicular cross-section, where the bank is 4 m high, the upper width is 7 m, and the legs are 10 m long. - Isosceles trapezoid
The bases of the isosceles trapezoid are in the ratio of 5:3. The arms have a length of 5 cm and height = 4.8 cm. Calculate the circumference and area of a trapezoid. - Intersection 81594
Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA? - Temperature and volume
The pool with a length of l = 50 m and a width of s = 15 m has a depth of h1 = 1.2 m at the shallowest part of the wall. The depth then gradually increases to a depth of h2 = 1.5 m in the middle of the pool. = 4.5 m walls in the deepest part of the pool. - Determine 81756
The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base. - Height—the 6183
In the isosceles trapezoid ABCD, the base length is a = 10cm, c = 6cm, and the arm's length is 4cm. Calculate its height—the result round to tenths. - Isosceles trapezoid
Find the area of an isosceles trapezoid; if the bases are 12 cm and 20 cm, the arm's length is 16 cm. - Isosceles trapezoid
What is the height of an isosceles trapezoid, the base of which is 11 cm and 8 cm long, and whose legs measure 2.5 cm? - Isosceles trapezoid 3
In the isosceles trapezoid ABCD, calculate the unknown side length "a" and its area. Side b = d = 50 cm, c = 20 cm, height = 48 cm. - Difference 79094
Trapezoid, gamma angle=121°, alpha angle=2 thirds of delta angle. Calculate the angle difference alpha, beta - Trapezoid 61394
Sestroj trapezoid ABCD, if a = 8cm, b = 5cm, alpha = 60 °, beta = 75 ° - The rectangular
The rectangular trapezoid has bases 15 dm and 8 dm long, and the length of the inclined arm is 12 dm. How long is the other arm of the trapezoid? - Isosceles trapezium
Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm. - Trapezoid ABCD
Calculate the perimeter of trapezoid ABCD if we know the side c=12, b=19, which is also a height, and side d=32. - Four sides of trapezoid In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles.
- KLMN
In the KLMN trapezoid is given this information: 1. segments KL and MN are parallel 2. segments KL and KM have the same length 3. segments KN, NM, and ML have the same length. Determine the size of the angle KMN. - MO Z9–I–2 - 2017
VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid. - Right trapezoid
Calculate the area of a rectangular trapezoid whose perpendicular arm is 27 mm long and the bases are 33 mm and 19 mm long.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
