Triangle practice problems - page 12 of 126
Number of problems found: 2501
- Triangle 42
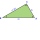 Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=?
Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=? - Calculate 2
 Calculate the largest angle of the triangle whose sides are 5.2cm, 3.6cm, and 2.1cm
Calculate the largest angle of the triangle whose sides are 5.2cm, 3.6cm, and 2.1cm - Triangle angles
 In a triangle, ABC, the interior angle at vertex C is twice the internal angle at point A. The outer angle at point B measured 117 degrees. How big is the external angle at vertex A?
In a triangle, ABC, the interior angle at vertex C is twice the internal angle at point A. The outer angle at point B measured 117 degrees. How big is the external angle at vertex A? - Isosceles triangle and cosine
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - In triangle 2
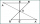 In triangle XYZ, if it measures angle X=40° and measures angle Y=75°. Which is the longest side of the triangle, and why?
In triangle XYZ, if it measures angle X=40° and measures angle Y=75°. Which is the longest side of the triangle, and why? - Main/central vertex
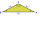 ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B?
ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B? - Sss triangle
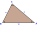 Calculate the area and heights in the triangle ABC by sides a = 8cm, b = 11cm, c = 12cm
Calculate the area and heights in the triangle ABC by sides a = 8cm, b = 11cm, c = 12cm - A triangle
 A triangle has one angle of 63.1°, and the other two are in the ratio of 2:5. What are the measurements of the two angles?
A triangle has one angle of 63.1°, and the other two are in the ratio of 2:5. What are the measurements of the two angles? - Thomas
 Thomas lives 400 meters away from Samko, Robo from Thomas also 400 m, and Samko from Robo 500. Anton lives 300 meters away from Robo, further than Samko. How far away lives Anton from Rob?
Thomas lives 400 meters away from Samko, Robo from Thomas also 400 m, and Samko from Robo 500. Anton lives 300 meters away from Robo, further than Samko. How far away lives Anton from Rob? - Triangle - ratio
 Change the triangle in a ratio of 3:4 The length of the sides of a triangle: a = 7 cm b = 6 cm c = 5 cm
Change the triangle in a ratio of 3:4 The length of the sides of a triangle: a = 7 cm b = 6 cm c = 5 cm - Alfa, beta, gama
 In the ABC triangle, is the size of the internal angle BETA 8 degrees larger than the size of the internal angle ALFA and the size of the internal angle GAMA is twice the size of the angle BETA? Determine the size of the interior angles of the triangle AB
In the ABC triangle, is the size of the internal angle BETA 8 degrees larger than the size of the internal angle ALFA and the size of the internal angle GAMA is twice the size of the angle BETA? Determine the size of the interior angles of the triangle AB - Arm-leg
 Calculate the length of the base of an isosceles triangle with a circumference of 224 cm if the arm length is 68 cm.
Calculate the length of the base of an isosceles triangle with a circumference of 224 cm if the arm length is 68 cm. - Calculate 82878
 Calculate in degrees the size of the acute angle made by the hands of the clock at half past six.
Calculate in degrees the size of the acute angle made by the hands of the clock at half past six. - Determine 81572
 In one triangle, one angle is 43°, and the second is 15° less than the third. Determine the unknown angles of the triangle.
In one triangle, one angle is 43°, and the second is 15° less than the third. Determine the unknown angles of the triangle. - Perimeter 80853
 The lengths of the sides of the triangle are in the ratio 7:6:4. The shortest side is 36 cm. What is the perimeter in cm of this triangle?
The lengths of the sides of the triangle are in the ratio 7:6:4. The shortest side is 36 cm. What is the perimeter in cm of this triangle? - Different 42191
 How many different triangles with vertices formed by points A, B, C, D, E, and F can we create?
How many different triangles with vertices formed by points A, B, C, D, E, and F can we create? - Circumference + sides
 The lengths of the triangle sides are in the ratio of 3:5:7. Its circumference is 45 cm. Find its lengths.
The lengths of the triangle sides are in the ratio of 3:5:7. Its circumference is 45 cm. Find its lengths. - Magnitude 23271
 In an isosceles triangle, the angle at the primary vertex is 20 ° smaller than twice the magnitude of the angle at the base. What are the interior angles of a triangle?
In an isosceles triangle, the angle at the primary vertex is 20 ° smaller than twice the magnitude of the angle at the base. What are the interior angles of a triangle? - Triangular flowerbed
 A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m?
A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m? - Three altitudes
 A triangle with altitudes 4, 5, and 6 cm is given. Calculate the lengths of all medians and all sides in a triangle.
A triangle with altitudes 4, 5, and 6 cm is given. Calculate the lengths of all medians and all sides in a triangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
