Volume + right triangle - practice problems
Number of problems found: 289
- The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Quadrilateral 83307
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
- Calculate 83044
 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Calculate 82690
 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Equilateral 82576
 Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm.
Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm. - ABCDEFGH 82499
 In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
- Right-angled 82416
 What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²? - Quadrilateral 82066
 Calculate the volume of a regular quadrilateral pyramid with a square base of side a = 3 cm and side length b = 7 cm.
Calculate the volume of a regular quadrilateral pyramid with a square base of side a = 3 cm and side length b = 7 cm. - Cantilevers 81937
 Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm.
Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm. - Equilateral 81222
 A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere?
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - Equilateral 81142
 The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body.
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body.
- Circumference of edges
 The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume.
The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume. - Calculate 81034
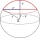 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - Fifty-meter 80722
 Calculate how many hectoliters of water can fit in a fifty-meter sloped pool; if the smallest depth is 1.2 m and the largest depth is 3 m, the width of the pool is 20 m.
Calculate how many hectoliters of water can fit in a fifty-meter sloped pool; if the smallest depth is 1.2 m and the largest depth is 3 m, the width of the pool is 20 m. - Perpendicular 79804
 A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he
A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he - One-third 77724
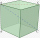 The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid?
The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
