Volume + expression of a variable from the formula - practice problems - page 10 of 32
Number of problems found: 630
- Barrel-shaped 40601
 The barrel-shaped cylinder has a volume of 9.42 hl, and the inner diameter of the bottom is 12 dm. Calculate the area of the barrel shell in m². Solve in general first.
The barrel-shaped cylinder has a volume of 9.42 hl, and the inner diameter of the bottom is 12 dm. Calculate the area of the barrel shell in m². Solve in general first. - Surface and volume - cube
 Find the surface and volume of a cube whose wall diagonal is 5 cm long.
Find the surface and volume of a cube whose wall diagonal is 5 cm long. - The volume
 The volume of the cone is 94.2 dm³, and the radius of the base is 6 dm. Calculate the surface of the cone.
The volume of the cone is 94.2 dm³, and the radius of the base is 6 dm. Calculate the surface of the cone. - The volume
 The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
- Pharmacist
 The pharmacist had a 12 liters vessel herbal lotion, which contained a 30% active ingredient. Her assistant poured 18 liters of herbal lotion containing 45% of the active ingredient into a container. What percentage of herbal lotion was produced?
The pharmacist had a 12 liters vessel herbal lotion, which contained a 30% active ingredient. Her assistant poured 18 liters of herbal lotion containing 45% of the active ingredient into a container. What percentage of herbal lotion was produced? - Truncated pyramid
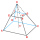 Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm. - The cylinder
 In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder.
In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder. - Gravitational 38843
 An aluminum plate with a volume of 200 cm³ sinks in water. Determine the gravitational force exerted by the Earth on the plate. Determine the buoyant force that acts on a plate immersed in water. Compare the magnitudes of these forces and justify whether
An aluminum plate with a volume of 200 cm³ sinks in water. Determine the gravitational force exerted by the Earth on the plate. Determine the buoyant force that acts on a plate immersed in water. Compare the magnitudes of these forces and justify whether - Rotary cylinder
 In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
- Pentagonal pyramid
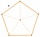 The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid.
The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid. - Truncated cone
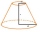 Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm, and side s = 10 cm.
Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm, and side s = 10 cm. - Calculate 38701
 Calculate the surface and volume of the cut rotating cone with base radii of 14cm and 8cm height of 11cm.
Calculate the surface and volume of the cut rotating cone with base radii of 14cm and 8cm height of 11cm. - Cube-shaped container
 The cube-shaped container has a height of 52 cm and a square base. The container was filled to the brim with water, and then we immersed a metal cube in it, which caused 2.7 l of water to flow out of the container. After removing the cube from the water,
The cube-shaped container has a height of 52 cm and a square base. The container was filled to the brim with water, and then we immersed a metal cube in it, which caused 2.7 l of water to flow out of the container. After removing the cube from the water, - Isosceles + prism
 Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm
Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm
- Calculate 38073
 1. Calculate the volume of a cube whose edge is 3.6 dm long. 2. Calculate the edge's size if you know its surface S = 2166 mm².
1. Calculate the volume of a cube whose edge is 3.6 dm long. 2. Calculate the edge's size if you know its surface S = 2166 mm². - Three cubes
 Two cube-shaped boxes with edges a = 70 cm; b = 90 cm must be replaced by one cube-shaped box. What will be its edge?
Two cube-shaped boxes with edges a = 70 cm; b = 90 cm must be replaced by one cube-shaped box. What will be its edge? - Cuboid - ratio
 Find the volume of a block whose dimensions are in the ratio 2: 3: 4 and the surface is 117 dm².
Find the volume of a block whose dimensions are in the ratio 2: 3: 4 and the surface is 117 dm². - The base 2
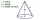 The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14
The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14 - Spherical section cut
 Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Tip: Our volume units converter will help you convert volume units. Volume - math word problems. Expression of a variable from the formula - math word problems.
